(1)人教版八年级数学下册92页第14题是这样叙述的:如图1,▱ABCD中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?根据习题背景,写出面积相等的一对平行四边形的名称为和;(2)如图2,点P为▱ABCD内一点,过点P分别作AD、AB的平行线分别交▱ABCD的四边于点E、F、G、H.已知S▱BHPE=3,S▱PFDG=5,则S△PAC=;(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形面积的和
2019-05-22
(1)人教版八年级数学下册92页第14题是这样叙述的:如图1,▱ABCD中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?
根据习题背景,写出面积相等的一对平行四边形的名称为______和______;
(2)如图2,点P为▱ABCD内一点,过点P分别作AD、AB的平行线分别交▱ABCD的四边于点E、F、G、H.已知S▱BHPE=3,S▱PFDG=5,则S△PAC=______;
(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,则菱形EFGH的周长为______.
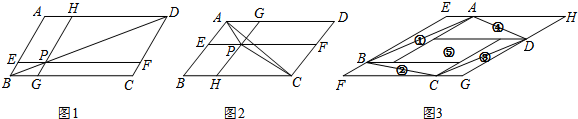
根据习题背景,写出面积相等的一对平行四边形的名称为______和______;
(2)如图2,点P为▱ABCD内一点,过点P分别作AD、AB的平行线分别交▱ABCD的四边于点E、F、G、H.已知S▱BHPE=3,S▱PFDG=5,则S△PAC=______;
(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,则菱形EFGH的周长为______.

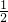 S▱ABCD=S△PAG+S△PCF+S▱PFDG-
S▱ABCD=S△PAG+S△PCF+S▱PFDG-