某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答:(1)如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EFGH;(填“>”“=”或“<”)(2)如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证: EF GH = AD AB
2019-06-02
某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答:
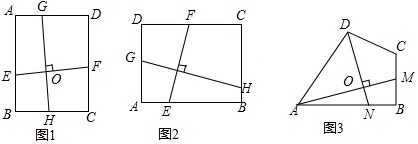
(1)如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EF___GH;(填“>”“=”或“<”)
(2)如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证: = ;
(3)如图3,四边形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,点M,N分别在边BC,AB上,求 的值.
优质解答
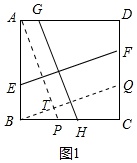
(1)如图1中,过点A作AP∥GH,交BC于P,过点B作BQ∥EF,交CD于Q,交BQ于T.
∵四边形ABCD是正方形,
∴AB∥DC,AD∥BC.AB=BC,∠ABP=∠C=90°
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=GH,EF=BQ.
又∵GH⊥EF,
∴AP⊥BQ,
∴∠PBT+∠ABT=90°,∠ABT+∠BAT=90°,
∴∠CBQ=∠BAT,
在△ABP和△BCQ中,
,
∴△ABP≌△BCQ,
∴AP=BQ,
∴EF=GH,
故答案为=.
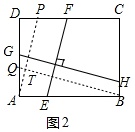
(2)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图2,
∵四边形ABCD是矩形,∴AB∥DC,AD∥BC.
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ.
又∵GH⊥EF,∴AP⊥BQ,
∴∠QAT+∠AQT=90°.
∵四边形ABCD是矩形,∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA.
∴△PDA∽△QAB,
∴=,
∴=;
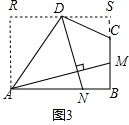
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,
则四边形ABSR是平行四边形.
∵∠ABC=90°,∴▱ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS.
∵AM⊥DN,
∴由(1)中的结论可得=,
设SC=x,则AR=BS=3+x,
∵∠ADC=∠R=∠S=90°,
∴∠ADR+∠RAD=90°,∠ADR+∠SDC=90°,
∴∠RAD=∠CDS,
∴△ARD∽△DSC,
∴====,
∴DR=x,DS=(x+3),
在Rt△ARD中,∵AD2=AR2+DR2,
∴7.52=(x+3)2+(x)2,
整理得13x2+24x-189=0,解得x=3或-,
∴AR=6,AB=RS=,
∴==.
(1)如图1中,过点A作AP∥GH,交BC于P,过点B作BQ∥EF,交CD于Q,交BQ于T.

∵四边形ABCD是正方形,
∴AB∥DC,AD∥BC.AB=BC,∠ABP=∠C=90°
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=GH,EF=BQ.
又∵GH⊥EF,
∴AP⊥BQ,
∴∠PBT+∠ABT=90°,∠ABT+∠BAT=90°,
∴∠CBQ=∠BAT,
在△ABP和△BCQ中,
,
∴△ABP≌△BCQ,
∴AP=BQ,
∴EF=GH,
故答案为=.
(2)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图2,

∵四边形ABCD是矩形,∴AB∥DC,AD∥BC.
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ.
又∵GH⊥EF,∴AP⊥BQ,
∴∠QAT+∠AQT=90°.
∵四边形ABCD是矩形,∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA.
∴△PDA∽△QAB,
∴=,
∴=;
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,

则四边形ABSR是平行四边形.
∵∠ABC=90°,∴▱ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS.
∵AM⊥DN,
∴由(1)中的结论可得=,
设SC=x,则AR=BS=3+x,
∵∠ADC=∠R=∠S=90°,
∴∠ADR+∠RAD=90°,∠ADR+∠SDC=90°,
∴∠RAD=∠CDS,
∴△ARD∽△DSC,
∴====,
∴DR=x,DS=(x+3),
在Rt△ARD中,∵AD2=AR2+DR2,
∴7.52=(x+3)2+(x)2,
整理得13x2+24x-189=0,解得x=3或-,
∴AR=6,AB=RS=,
∴==.
相关问答
- 理科实验班数学问题(分解因式)这道题以前做
- 一道数学问题 一节数学实践活动课上.一节数
- (1)班同学上数学活动课,利用角尺平分一个
- 数学题帮忙算下我校四年级学生开展了户外拓展
- 在线等,急!~ 谢谢!~ 数学拓展题.三(
- 人教版六年级数学53页拓展空间第2题怎么做
- 小学问题,紧急求助!六一儿童节期间,书店搞
- 请完整的填入试题,以便老师快速的帮你解答.
- 六一儿童节期间,书店搞促销活动,儿童书店所
- “六一”儿童节期间,书店搞促销活动.儿童书
- 请用六年级百分数应用知识破解.第一题;六一
- “六一”儿童节期间,书店搞促销活动儿童书店
- 一道数学题,讲清楚,不要假设,不要方程"六
- 儿童书店所有书一律7折销售 新华书店所有图
- 李老师编写了一本《趣味数学》,获得稿费38
- 冀教版三年级数学一课一练第25页趣味乐园




