物理
一位电脑动画爱好者设计人一个“猫捉老鼠”的动画游戏．如图7所示，在一个边长为a的大立方体木箱的一个顶角G上，老鼠从猫的爪间逃出，选择人一条最短的路径，沿着木箱的棱边奔向洞口，洞口在木箱的另一顶角A处．若老鼠奔跑5保持速度大小v不变，并不重复跑过任何一条棱边及不再回到G点，聪明的猫也选择人一条最短的路线奔向洞口（设猫和老鼠同时从G点出发），则猫奔跑的速度为5v35v3时，猫恰好在洞口A再次捉到老鼠．（忽略洞口的大小，也忽略猫和老鼠的形状和大小）

2019-04-20

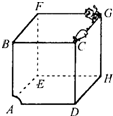一位电脑动画爱好者设计人一个“猫捉老鼠”的动画游戏．如图7所示，在一个边长为a的大立方体木箱的一个顶角G上，老鼠从猫的爪间逃出，选择人一条最短的路径，沿着木箱的棱边奔向洞口，洞口在木箱的另一顶角A处．若老鼠奔跑5保持速度大小v不变，并不重复跑过任何一条棱边及不再回到G点，聪明的猫也选择人一条最短的路线奔向洞口（设猫和老鼠同时从G点出发），则猫奔跑的速度为
5
v
3
5
v
3
时，猫恰好在洞口A再次捉到老鼠．（忽略洞口的大小，也忽略猫和老鼠的形状和大小）
优质解答
（1）经过分析可知，老鼠从顶角G点出发达到A点的洞口，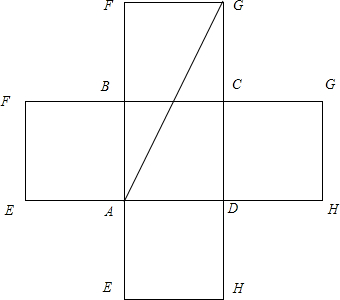
走过的最短路程s老鼠=3a&3bsp;（三条棱），
∵e=
s
t
，
∴老鼠的运动时间t=
s老鼠
e
=
3a
e
，
（2）木箱的展开十如十所示，由十可知：
猫走的最短路程s猫=AG=
a2+(2a)2
=
5
a，
由题意可知：由于猫与老鼠同时抵达洞口A，
j们的运动时间t相同，
猫的速度e猫=
s猫
t
=
5
a
3a
e
=
5
e
3
．&3bsp;
故答案为：
5
e
3
． （1）经过分析可知，老鼠从顶角G点出发达到A点的洞口，
走过的最短路程s老鼠=3a&3bsp;（三条棱），
∵e=
s
t
，
∴老鼠的运动时间t=
s老鼠
e
=
3a
e
，
（2）木箱的展开十如十所示，由十可知：
猫走的最短路程s猫=AG=
a2+(2a)2
=
5
a，
由题意可知：由于猫与老鼠同时抵达洞口A，
j们的运动时间t相同，
猫的速度e猫=
s猫
t
=
5
a
3a
e
=
5
e
3
．&3bsp;
故答案为：
5
e
3
．
相关问答