优质解答
如图:已知:CD平分AB,且CD=AD=BD,
求证:△ABC是直角三角形.
证明:∵AD=CD,
∴∠A=∠1.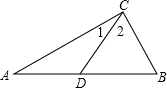
同理∠2=∠B.
∵∠2+∠B+∠A+∠1=180°,
即2(∠1+∠2)=180°,
∴∠1+∠2=90°,
即:∠ACB=90°,
∴△ABC是直角三角形. 如图:已知:CD平分AB,且CD=AD=BD,
求证:△ABC是直角三角形.
证明:∵AD=CD,
∴∠A=∠1.
同理∠2=∠B.
∵∠2+∠B+∠A+∠1=180°,
即2(∠1+∠2)=180°,
∴∠1+∠2=90°,
即:∠ACB=90°,
∴△ABC是直角三角形.
求证:△ABC是直角三角形.
证明:∵AD=CD,
∴∠A=∠1.

同理∠2=∠B.
∵∠2+∠B+∠A+∠1=180°,
即2(∠1+∠2)=180°,
∴∠1+∠2=90°,
即:∠ACB=90°,
∴△ABC是直角三角形. 如图:已知:CD平分AB,且CD=AD=BD,
求证:△ABC是直角三角形.
证明:∵AD=CD,
∴∠A=∠1.

同理∠2=∠B.
∵∠2+∠B+∠A+∠1=180°,
即2(∠1+∠2)=180°,
∴∠1+∠2=90°,
即:∠ACB=90°,
∴△ABC是直角三角形.