精选问答
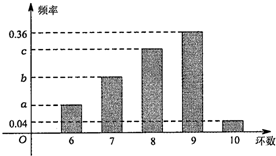（2014•泉州模拟）已知某射击队员每次射击击中目标靶的环数都在6环以上（含6环），据统计数据绘制得到的频率分布条形图如图所示，其中a，b，c依次构成公差为0.1的等差数列，若视频率为概率，且该队员每次射击相互独立，试解答下列问题：（Ⅰ）求a，b，c的值，并求该队员射击一次，击中目标靶的环数ξ的分布列和数学期望Eξ；（Ⅱ）若该射击队员在10次的射击中，击中9环以上（含9环）的次数为k的概率为P（X=k），试探究：当k为何值时，P（X=k）取得最大值？

2020-01-04

（2014•泉州模拟）已知某射击队员每次射击击中目标靶的环数都在6环以上（含6环），据统计数据绘制得到的频率分布条形图如图所示，其中a，b，c依次构成公差为0.1的等差数列，若视频率为概率，且该队员每次射击相互独立，试解答下列问题：
（Ⅰ）求a，b，c的值，并求该队员射击一次，击中目标靶的环数ξ的分布列和数学期望Eξ；
（Ⅱ）若该射击队员在10次的射击中，击中9环以上（含9环）的次数为k的概率为P（X=k），试探究：当k为何值时，P（X=k）取得最大值？
优质解答
（1）依题意，得a+b+c=0.6，
即a+a+0.1+a+0.2=0.6，解得a=0.1，
∴b=0.2，c=0.3，
∴该队员射击一次击中目标靶的环数ξ的分布列为：
 ξ 6 78  9 10
 P 0.10.2  0.30.36  0.04
Eξ=6×0.1+7×0.2+8×0.3+9×0.36+10×0.04=8.04．
（Ⅱ）记事件A：“该队员进行一次射击，击中9环”，
事件B：“该队员进行一次射击，击中10环”，
则事件“该队员进行一次射击，击中9环以上（含9环）”为A+B，
∵A，B互斥，且P（A）=0.36，P（B）=0.04，
∴P（A+B）=P（A）+P（B）=0.4，
∴该射击队员在10射击中，击中9环以上（含9环）的次数为k的概率：
P（X=k）=
C
k
10
×0．4k×0．610−k，k=0，1，2，…，10），
当k≥1时，k∈N*时，
P(X＝k)
P(X＝k−1)
＝
C
k
10
×0．4k×0．610−k
C
k−1
10
×0．4k−1×0．610−k+1
=
2(11−k)
3k
，
令
P(X＝k)
P(X＝k−1)
＞1，解得k＜
22
5
，
∴1≤k≤4时，P（X=k-1）＜P（X=k），
5≤k≤10时，P（X=＞P（X=k）．
综上，当k=4时，P（X=k）取得最大值． （1）依题意，得a+b+c=0.6，
即a+a+0.1+a+0.2=0.6，解得a=0.1，
∴b=0.2，c=0.3，
∴该队员射击一次击中目标靶的环数ξ的分布列为：
 ξ 6 78  9 10
 P 0.10.2  0.30.36  0.04
Eξ=6×0.1+7×0.2+8×0.3+9×0.36+10×0.04=8.04．
（Ⅱ）记事件A：“该队员进行一次射击，击中9环”，
事件B：“该队员进行一次射击，击中10环”，
则事件“该队员进行一次射击，击中9环以上（含9环）”为A+B，
∵A，B互斥，且P（A）=0.36，P（B）=0.04，
∴P（A+B）=P（A）+P（B）=0.4，
∴该射击队员在10射击中，击中9环以上（含9环）的次数为k的概率：
P（X=k）=
C
k
10
×0．4k×0．610−k，k=0，1，2，…，10），
当k≥1时，k∈N*时，
P(X＝k)
P(X＝k−1)
＝
C
k
10
×0．4k×0．610−k
C
k−1
10
×0．4k−1×0．610−k+1
=
2(11−k)
3k
，
令
P(X＝k)
P(X＝k−1)
＞1，解得k＜
22
5
，
∴1≤k≤4时，P（X=k-1）＜P（X=k），
5≤k≤10时，P（X=＞P（X=k）．
综上，当k=4时，P（X=k）取得最大值．
相关问答