教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲、乙两个同轨班级进行实验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面2×2列联表:(单位:人)优秀人数非优秀人数总计甲班22830乙班81220总计302050(1)能否据此判断有97.5%的把握认为加强语文阅读理解训练与提高数学应用题得分率有关?(2)经过多次测试后,小明正确解答一道数学题所用的时间在5-7分钟,小刚正确解答一道数学题所用的时间
2019-04-29
教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲、乙两个同轨班级进行实验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面2×2列联表:(单位:人)
| 优秀人数 | 非优秀人数 | 总计 |
| 甲班 | 22 | 8 | 30 |
| 乙班 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为加强语文阅读理解训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学题所用的时间在5-7分钟,小刚正确解答一道数学题所用的时间在6-8分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
(3)现从乙班成绩优秀的8名同学中任意抽取两人,并对他们的大题情况进行全程研究,记A、B两人中被抽到的人数为X,求X的分布列及数学期望E(X).
附表及公式
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
.
优质解答
(1)由表中数据计算K2的观测值:K2=| 50×(22×12-8×8)2 |
| 30×20×30×20 |
≈5.556>5.024.
所以根据统计有97.5%的把握认为加强语文阅读理解训练与提高数学应用题得分率有关;
(2)设小明与小刚解答这道题所用的时间分别为x、y分钟,
则基本事件所满足的条件是所表示的平面区域;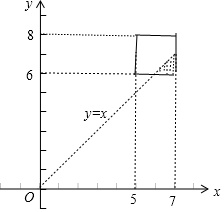
设事件A为“小刚比小明先解答完试题”,则满足的区域为x>y;
由几何概型的概率,计算P(A)==,
∴小刚比小明先正确解答完的概率是;
(3)根据题意,X的所有可能取值为0,1,2,则P(X=0)==,P(X=1)==,P(X=2)==;
∴X的分布列为:
X的数学期望为EX=所以E(X)=0×+1×+2×| 1 |
| 28 | <
(1)由表中数据计算K2的观测值:K2=| 50×(22×12-8×8)2 |
| 30×20×30×20 |
≈5.556>5.024.
所以根据统计有97.5%的把握认为加强语文阅读理解训练与提高数学应用题得分率有关;
(2)设小明与小刚解答这道题所用的时间分别为x、y分钟,
则基本事件所满足的条件是所表示的平面区域;
设事件A为“小刚比小明先解答完试题”,则满足的区域为x>y;
由几何概型的概率,计算P(A)==,
∴小刚比小明先正确解答完的概率是;
(3)根据题意,X的所有可能取值为0,1,2,则P(X=0)==,P(X=1)==,P(X=2)==;
∴X的分布列为:
X的数学期望为EX=所以E(X)=0×+1×+2×


