优质解答
(1)当身高不小于160cm时,设y与x的函数解析式为y=kx+b,由题意得,
 ,
,
解得: .
.
故y与x的函数解析式为:y=0.9x-90.
(2)当x=163时,
y=0.9×163-90,
=56.7kg;
(3)∵55÷(1+10%)=50kg,55÷(1-10%)= kg,
kg,
∴y=50时,x-105=50,解得,x=155,
当y= 时.0.9x-90=
时.0.9x-90= ,解得x=167
,解得x=167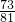 ≈167,
≈167,
故这个人的在155cm到167之间. (1)当身高不小于160cm时,设y与x的函数解析式为y=kx+b,由题意得,
 ,
,
解得: .
.
故y与x的函数解析式为:y=0.9x-90.
(2)当x=163时,
y=0.9×163-90,
=56.7kg;
(3)∵55÷(1+10%)=50kg,55÷(1-10%)= kg,
kg,
∴y=50时,x-105=50,解得,x=155,
当y= 时.0.9x-90=
时.0.9x-90= ,解得x=167
,解得x=167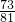 ≈167,
≈167,
故这个人的在155cm到167之间.
 ,
,解得:
 .
.故y与x的函数解析式为:y=0.9x-90.
(2)当x=163时,
y=0.9×163-90,
=56.7kg;
(3)∵55÷(1+10%)=50kg,55÷(1-10%)=
 kg,
kg,∴y=50时,x-105=50,解得,x=155,
当y=
 时.0.9x-90=
时.0.9x-90= ,解得x=167
,解得x=167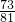 ≈167,
≈167,故这个人的在155cm到167之间. (1)当身高不小于160cm时,设y与x的函数解析式为y=kx+b,由题意得,
 ,
,解得:
 .
.故y与x的函数解析式为:y=0.9x-90.
(2)当x=163时,
y=0.9×163-90,
=56.7kg;
(3)∵55÷(1+10%)=50kg,55÷(1-10%)=
 kg,
kg,∴y=50时,x-105=50,解得,x=155,
当y=
 时.0.9x-90=
时.0.9x-90= ,解得x=167
,解得x=167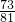 ≈167,
≈167,故这个人的在155cm到167之间.