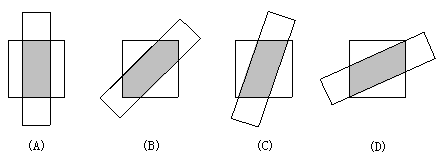
分析:A、阴影部分是长方形,所以长方形的面积等于长和宽的乘积;
B、如图,设阴影部分等腰直角的腰为x,根据勾股定理求出x的值,所以,阴影部分的面积等于正方形的面积减去俩个空白三角形的面积;
C、图C,逆时针旋转90°从后面看,可与图D对比,因为图C阴影部分的倾斜度比图D阴影部分的倾斜度小,所以,图C中四边形的底比图D中四边形的底小,两图为等高不等底,所以图C阴影部分的面积小于图D阴影部分的面积;
D、图D,设阴影部分平行四边形的底为x,根据正方形的面积=阴影部分的面积+两个空白三角形的面积,求出x的值,再得出阴影部分的面积;
图A、图C、图D中阴影部分四边形为等高不等底,因为倾斜度不同,所以图D中阴影部分的底最大,面积也就最大;因此,只要比较图B和图D阴影的面积大小,可得到图B阴影部分的面积最大.
A、S
阴影 =2×4=8(cm
2 );
B如图所示:根据勾股定理知,2x
2 =4,所以x=
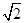
,S
阴影 =4×4-2×
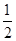
×(4-
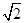
)(4-
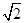
)=8
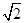
-2(cm
2 );
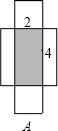


C、图C,逆时针旋转90°,并从后面看,可与图D对比,因为图C的倾斜度比图D的倾斜度小,所以,图C的底比图D的底小,两图为等高不等底,所以图C阴影部分的面积小于图D阴影部分的面积.
D、如图:设阴影部分平行四边形的底为x,所以,直角三角形的短直角边是
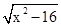
因为正方形的面积=阴影部分的面积+两个空白三角形的面积,
所以,
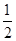
×4×
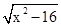
×2+2x=16,解得x=
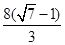
,S
阴影 =2×
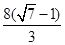
=
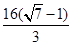
因为,
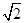
≈1.414,
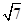
≈2.646,所以,8
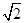
-2≈9.312,
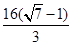
≈8.775;
即8
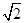
-2>
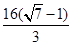
,图B阴影的面积大于图D阴影的面积;
又因为图A、图C、图D中阴影部分四边形为等高不等底,因为图D阴影的倾斜度最大,所以图D中阴影部分的底最大;
故选B
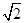 ,S 阴影 =4×4-2×
,S 阴影 =4×4-2×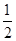 ×(4-
×(4-
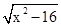
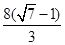 ,S 阴影 =2×
,S 阴影 =2×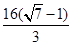
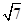 ≈2.646,所以,8
≈2.646,所以,8