优质解答
(1)如图所示:
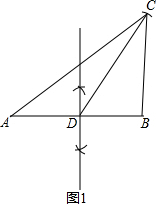

(2)证明:取AC中点D,连接BD,
∵AC=2,∴CD=1,
∵∠C=90°,BC=
,
∴BD=
=2,
∴AC=BD,
∴△ABC是“趣味三角形”;
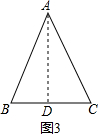 (3)如图3所示:取BC的中点D,连接AD,
(3)如图3所示:取BC的中点D,连接AD,
当AD=BC时,△ABC是“趣味三角形”,
∵AB=AC=4,∴BD=DC=
BC,
在Rt△ABD中,BD2+AD2=AB2,
∴(
BC)2+BC2=42,
解得:BC=
=
,
如图4,取AC中点D,连接BD,
当BD=AC时,△ABC是“趣味三角形”,
∵AB=AC=4,
∴AD=DC=2,
由勾股定理得:
BC2-CE2=AB2-AE2,
解得:BC=
=2
.
(1)如图所示:


(2)证明:取AC中点D,连接BD,
∵AC=2,∴CD=1,
∵∠C=90°,BC=
,
∴BD=
=2,
∴AC=BD,
∴△ABC是“趣味三角形”;
 (3)如图3所示:取BC的中点D,连接AD,
(3)如图3所示:取BC的中点D,连接AD,
当AD=BC时,△ABC是“趣味三角形”,
∵AB=AC=4,∴BD=DC=
BC,
在Rt△ABD中,BD2+AD2=AB2,
∴(
BC)2+BC2=42,
解得:BC=
=
,
如图4,取AC中点D,连接BD,
当BD=AC时,△ABC是“趣味三角形”,
∵AB=AC=4,
∴AD=DC=2,
由勾股定理得:
BC2-CE2=AB2-AE2,
解得:BC=
=2
.


(2)证明:取AC中点D,连接BD,
∵AC=2,∴CD=1,
∵∠C=90°,BC=
| 3 |
∴BD=
| BC2+CD2 |
∴AC=BD,
∴△ABC是“趣味三角形”;
 (3)如图3所示:取BC的中点D,连接AD,
(3)如图3所示:取BC的中点D,连接AD,当AD=BC时,△ABC是“趣味三角形”,
∵AB=AC=4,∴BD=DC=
| 1 |
| 2 |
在Rt△ABD中,BD2+AD2=AB2,
∴(
| 1 |
| 2 |
解得:BC=
|
8
| ||
| 5 |
如图4,取AC中点D,连接BD,

当BD=AC时,△ABC是“趣味三角形”,
∵AB=AC=4,
∴AD=DC=2,
由勾股定理得:
BC2-CE2=AB2-AE2,
解得:BC=
| 24 |
| 6 |


(2)证明:取AC中点D,连接BD,
∵AC=2,∴CD=1,
∵∠C=90°,BC=
| 3 |
∴BD=
| BC2+CD2 |
∴AC=BD,
∴△ABC是“趣味三角形”;
 (3)如图3所示:取BC的中点D,连接AD,
(3)如图3所示:取BC的中点D,连接AD,当AD=BC时,△ABC是“趣味三角形”,
∵AB=AC=4,∴BD=DC=
| 1 |
| 2 |
在Rt△ABD中,BD2+AD2=AB2,
∴(
| 1 |
| 2 |
解得:BC=
|
8
| ||
| 5 |
如图4,取AC中点D,连接BD,

当BD=AC时,△ABC是“趣味三角形”,
∵AB=AC=4,
∴AD=DC=2,
由勾股定理得:
BC2-CE2=AB2-AE2,
解得:BC=
| 24 |
| 6 |