(x<0)交于点A(-1,n).(1)求直线与双曲线的解析式.(2)连接OA,求∠OAB的正弦值.(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由.
2019-04-10
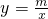 (x<0)交于点A(-1,n).
(x<0)交于点A(-1,n).
(1)求直线与双曲线的解析式.
(2)连接OA,求∠OAB的正弦值.
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由.
优质解答
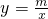 (x<0)得:m=5,
(x<0)得:m=5,
∴双曲线的解析式是:y=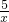 ;
;
(2)过点O作OM⊥AC于点M,
∵B点经过y轴,
∴x=0,
∴0-4=y,
∴y=4,
∴B(0,-4),
AO=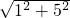 =
=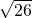 ,
,
∵OC=OB=4,
∴△OCB是等腰三角形,
∴∠OBC=∠OCB=45°,
∴在△OMB中 sin45°=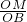 =
=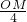 ,
,
∴OM=2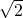 ,
,
∴在△AOM中,
sin∠OAB=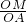
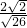 =
=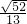 ;
;
(3)存在;
过点A作AN⊥y轴,垂足为点N,
则AN=1,BN=1,
则AB=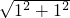 =
=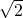 ,
,
∵OB=OC=4,
∴BC=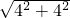 =4
=4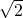 ,
,
∠OBC=∠OCB=45°,
∴∠OBA=∠BCD=135°,
∴△OBA∽△BCD或△OBA∽△DCB,
∴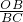 =
=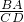 或
或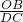 =
=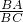 ,
,
∴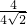 =
=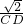 或
或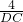 =
=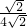 ,
,
∴CD=2或CD=16,
∴点D的坐标是(6,0)或(20,0).
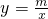 (x<0)得:m=5,
(x<0)得:m=5,
∴双曲线的解析式是:y=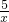 ;
;
(2)过点O作OM⊥AC于点M,
∵B点经过y轴,
∴x=0,
∴0-4=y,
∴y=4,
∴B(0,-4),
AO=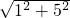 =
=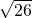 ,
,
∵OC=OB=4,
∴△OCB是等腰三角形,
∴∠OBC=∠OCB=45°,
∴在△OMB中 sin45°=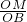 =
=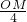 ,
,
∴OM=2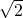 ,
,
∴在△AOM中,
sin∠OAB=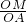
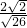 =
=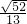 ;
;
(3)存在;
过点A作AN⊥y轴,垂足为点N,
则AN=1,BN=1,
则AB=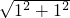 =
=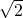 ,
,
∵OB=OC=4,
∴BC=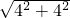 =4
=4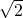 ,
,
∠OBC=∠OCB=45°,
∴∠OBA=∠BCD=135°,
∴△OBA∽△BCD或△OBA∽△DCB,
∴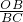 =
=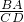 或
或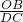 =
=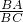 ,
,
∴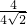 =
=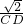 或
或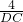 =
=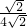 ,
,
∴CD=2或CD=16,
∴点D的坐标是(6,0)或(20,0).
相关问答
- 六年级下尖子生题库语文答案的73页的右图是
- 高中数学直线与圆的方程,只要公式
- 自学弹道学,需要要哪些数学和物理基础?恩,
- 高一数学必修3中最小二乘法求回归直线方程为
- 初中数学题 超简单,初二以下水平点P是直线
- 初二物理【同步解析与测试】练习册中40页最
- 右手螺旋定则具体内容是什么?有没有具体的图
- 用and连接的两个人称,谓语动词的形态和哪
- 英语语法问题.and连接并列句时,谓语动词
- 六年级数学判断题:用有正数和负数的直线可以
- 物理传送带问题要注意哪些要点?最好附上例题
- 一条直线上有两个点电荷,左边的是正电荷,右
- 怎么话电场线,什么时候是直线,什么时候是曲
- 高一物理必修一作业本P1-P11 的基础练
- 匀加速直线怎么表示路程一半的速度在匀加速直
- 初中几何语言的如何叙述比如,作辅助线时、连
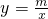 (x<0)交于点A(-1,n).
(x<0)交于点A(-1,n).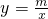 (x<0)交于点A(-1,n).
(x<0)交于点A(-1,n).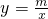 (x<0)得:m=5,
(x<0)得:m=5,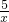 ;
;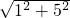 =
=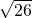 ,
,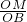 =
=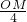 ,
,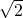 ,
,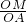
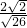 =
=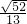 ;
;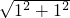 =
=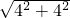 =4
=4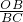 =
=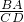 或
或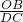 =
=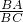 ,
,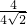 =
=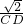 或
或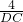 =
=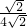 ,
,