好吧，自己解决，图像法：

先将分母同乘以a/d使分母的二次项系数也为a

整个个分式就乘以d/a

化为f(x)=((ax^2+bx+c)/(ax^2+(e*a/d)x+(f*a/d)))*d/a

设y1=ax^2+bx+c  y2=ax^2+(e*a/d)x+(f*a/d)

令y1=y2当且仅当b=e*a/d 时x在R上无解

此条件下    1当Δ1,Δ2均大于零时分6段讨论

            2当Δ1*Δ2＜0时分4段讨论

            3当Δ1,Δ2均小于零时分2段讨论

当b≠e*a/d时只有一解  如图

可分为8段（ABCDEFG）讨论  

根据二次函数斜率变化的特点可求解

具体各位大虾们自行解决

打下来太麻烦了

好吧，自己解决，图像法：

先将分母同乘以a/d使分母的二次项系数也为a

整个个分式就乘以d/a

化为f(x)=((ax^2+bx+c)/(ax^2+(e*a/d)x+(f*a/d)))*d/a

设y1=ax^2+bx+c  y2=ax^2+(e*a/d)x+(f*a/d)

令y1=y2当且仅当b=e*a/d 时x在R上无解

此条件下    1当Δ1,Δ2均大于零时分6段讨论

            2当Δ1*Δ2＜0时分4段讨论

            3当Δ1,Δ2均小于零时分2段讨论

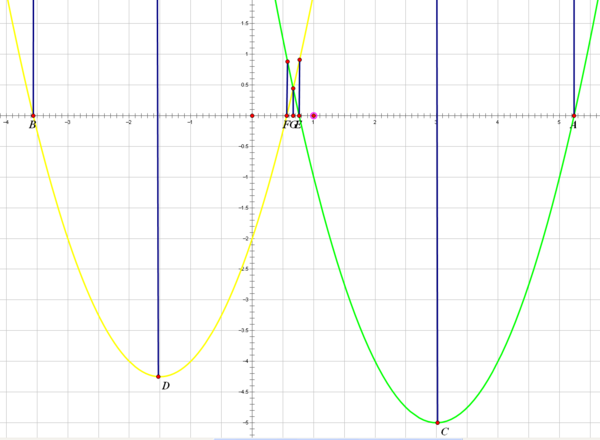
当b≠e*a/d时只有一解  如图

可分为8段（ABCDEFG）讨论  

根据二次函数斜率变化的特点可求解

具体各位大虾们自行解决

打下来太麻烦了