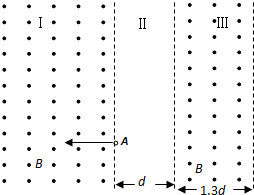
如图所示，一个带正电的粒子沿磁场边界从A点射入左侧磁场，粒子质量为m、电荷量为q，其中区域Ⅰ、Ⅲ内是垂直纸面向外的匀强磁场，左边区域足够大，右边区域宽度为1.3d，磁感应强度大小均为B，区域Ⅱ是两磁场间的无场区，两条竖直虚线是其边界线，宽度为d；粒子从左边界线A点射入磁场后，经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点，若粒子在左侧磁场中的半径为d，整个装置在真空中，不计粒子的重力．（1）求：粒子从A点射出到回到A点经历的时间t（2）若在区域Ⅱ内加一水平向右的匀强电场，粒子仍能回到A点，求：电场强度E．
2019-06-26
如图所示，一个带正电的粒子沿磁场边界从A点射入左侧磁场，粒子质量为m、电荷量为q，其中区域Ⅰ、Ⅲ内是垂直纸面向外的匀强磁场，左边区域足够大，右边区域宽度为1.3d，磁感应强度大小均为B，区域Ⅱ是两磁场间的无场区，两条竖直虚线是其边界线，宽度为d；粒子从左边界线A点射入磁场后，经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点，若粒子在左侧磁场中的半径为d，整个装置在真空中，不计粒子的重力．
（1）求：粒子从A点射出到回到A点经历的时间t
（2）若在区域Ⅱ内加一水平向右的匀强电场，粒子仍能回到A点，求：电场强度E．
优质解答
（1）因粒子从A点出发，经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点，由对称性可知粒子做圆周运动的半径为r=d，如右侧上图．
由Bqv=m得 v=
所以运行时间为 t==．
（2）设在区域Ⅱ内加速的粒子到Ⅲ区的速度为v1
由动能定理：qEd=mv12-mv2
设在区域Ⅲ内粒子做圆周运动的半径为r，分析粒子运动的轨迹，如图所示，
粒子沿半径为d的半圆运动至Ⅱ区，经电场加速后，在Ⅲ区又经半圆运动返回电场减速到边界线的A点，此时设AN=x
则：x=2（r-d）
此后，粒子每经历一次“回旋”，粒子沿边界线的距离就减小x，经过n次回旋后能返回A点．
必须满足：nx=2d（n=1、2、3、…）
求得：r＝d（n=1、2、3、…）
半径r太大可能从右边飞出磁场，所以必须满足下面条件：
由r≤1.3d，得：d≤1.3d即n≥≈3.33，（n=4、5、6、…）
由公式：Bqv1=m；得：v1＝，（n=4、5、6、…）
代入得：E＝（n=4、5、6、…）
答：
（1）粒子从A点射出到回到A点经历的时间t为．
（2）若在区域Ⅱ内加一水平向右的匀强电场，粒子仍能回到A点，电场强度E应为（n=4、5、6、…）．
（1）因粒子从A点出发，经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点，由对称性可知粒子做圆周运动的半径为r=d，如右侧上图．
由Bqv=m得 v=
所以运行时间为 t==．
（2）设在区域Ⅱ内加速的粒子到Ⅲ区的速度为v1
由动能定理：qEd=mv12-mv2
设在区域Ⅲ内粒子做圆周运动的半径为r，分析粒子运动的轨迹，如图所示，
粒子沿半径为d的半圆运动至Ⅱ区，经电场加速后，在Ⅲ区又经半圆运动返回电场减速到边界线的A点，此时设AN=x
则：x=2（r-d）
此后，粒子每经历一次“回旋”，粒子沿边界线的距离就减小x，经过n次回旋后能返回A点．
必须满足：nx=2d（n=1、2、3、…）
求得：r＝d（n=1、2、3、…）
半径r太大可能从右边飞出磁场，所以必须满足下面条件：
由r≤1.3d，得：d≤1.3d即n≥≈3.33，（n=4、5、6、…）
由公式：Bqv1=m；得：v1＝，（n=4、5、6、…）
代入得：E＝（n=4、5、6、…）
答：
（1）粒子从A点射出到回到A点经历的时间t为．
（2）若在区域Ⅱ内加一水平向右的匀强电场，粒子仍能回到A点，电场强度E应为（n=4、5、6、…）．