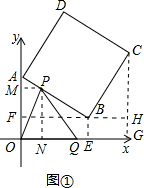
如图①，正方形ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A⇒B⇒C⇒D匀速运动，同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，设运动的时间为t秒．（1）当P点在边AB上运动时，点Q的横坐标x（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；（2）求正方形边长及顶点C的坐标；（3）在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标；（4）如果点P、

2019-12-16

下载本文

如图①，正方形ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A⇒B⇒C⇒D匀速运动，同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，设运动的时间为t秒．
（1）当P点在边AB上运动时，点Q的横坐标x（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；
（2）求正方形边长及顶点C的坐标；
（3）在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标；
（4）如果点P、Q保持原速度不变，当点P沿A⇒B⇒C⇒D匀速运动时，OP与PQ能否相等？若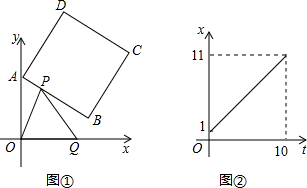

能，写出所有符合条件的t的值；若不能，请说明理由．

优质解答

（1）Q（1，0）（1分）Q的图象是一条直线，且过点（11，0）．
且点P运动速度每秒钟1个单位长度．（2分）

（2）过点B作BF⊥y轴于点F，BE⊥x轴于点E，则BF=8，OF=BE=4．
∴AF=10-4=6．
在Rt△AFB中，AB=

8 2 + 6 2

=10，（3分）
过点C作CG⊥x轴于点G，与FB的延长线交于点H．

∵∠ABC=90°，AB=BC，
∴△ABF≌△BCH．
∴BH=AF=6 CH=BF=8．
∴OG=FH=8+6=14，CG=8+4=12．
∴所求C点的坐标为（14，12）．（4分）

（3）过点P作PM⊥y轴于点M，PN⊥x轴于点N，
则△APM ∽ △ABF．
∴

AP

AB

=

AM

AF

=

MP

BF

，
∴

t

10

=

AM

6

=

MP

8

．
∴AM=

3

5

t，PM=

4

5

t，
∴PN=OM=10-

3

5

t，ON=PM=

4

5

t．
设△OPQ的面积为S（平方单位），
∴S=

1

2

×（10-

3

5

t）（1+t）=5+

47

10

t-

3

10

t² （0≤t≤10），（5分）
说明：未注明自变量的取值范围不扣分．
∵a=-

3

10

＜0 ，
∴当t=-

47

10

2×(-

3

10

)

=

47

6

时，△OPQ的面积最大．（6分）
此时P的坐标为（

94

15

，

53

10

）．（7分）

（4）OP与PQ相等，组成等腰三角形，即当P点的横坐标等于Q点的横坐标的一半时，
当P在BC上时，8+

3

5

（t-10）=

1

2

（t+1），解得：t=-15（舍去）
当P在CD上时，14-

4

5

（t-20）=

1

2

（t+1），解得：t=

295

13

，
即当t=

295

13

时，OP与PQ相等．
当P在BA上时，t=

5

3

，OP与PQ相等，（9分）
∴当t=

295

13

或t=

5

3

时，OP与PQ相等．