某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩分成六段[40，50），[50，60）…[90，100]后画出如下部分频率分布直方图，观察图形的信息，回答下列问题： （1）求第四小组的频率，并补全频率分布直方图；（2）估计这次考试的平均分和中位数（精确到0.01）；（3）从成绩是40～50分及90～100分的学生中选两人，记他们的成绩为x，y，求满足“|x-y|>10”的概率．
2019-05-05
某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩分成六段[40，50），[50，60）…[90，100]后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：
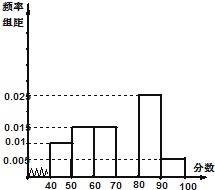
（1）求第四小组的频率，并补全频率分布直方图；
（2）估计这次考试的平均分和中位数（精确到0.01）；
（3）从成绩是40～50分及90～100分的学生中选两人，记他们的成绩为x，y，求满足“|x-y|>10”的概率．
优质解答
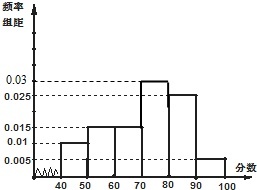（1）由频率分布直方图可知
第1、2、3、5、6小组的频率分别为：0.1、0.15、0.15、0.25、0.05，
所以第4小组的频率为：
1-0.1-0.15-0.15-0.25-0.05=0.3．
∴在频率分布直方图中第4小组的对应的矩形的高为0.03，
补全频率分布直方图对应图形如图所示：…（4分）
（2）由频率分布直方图可得平均分为：
0.1×45+0.15×55+0.15×65+0.3×75+0.25×85+0.05×95=71．…（6分）
第一、二、三组的频率之和为0.1+0.15+0.15=0.4
所以中位数=70+≈73.33…（8分）
（3）由频率分步直方图可得，成绩是40～50分的有40×0.1=4人，
90～100分的学生有40×0.05=2人，记取出的2个人的成绩为x，y，
“|x-y|>10”说明选出的2个人一个成绩在[40，50）内，
另一个在[50，60）内，
故满足“|x-y|>10”的选法有 4×2=8种，
而所有的取法有=15种，
故满足“|x-y|>10”的概率p=．…（14分）
（1）由频率分布直方图可知
第1、2、3、5、6小组的频率分别为：0.1、0.15、0.15、0.25、0.05，
所以第4小组的频率为：
1-0.1-0.15-0.15-0.25-0.05=0.3．
∴在频率分布直方图中第4小组的对应的矩形的高为0.03，
补全频率分布直方图对应图形如图所示：…（4分）
（2）由频率分布直方图可得平均分为：
0.1×45+0.15×55+0.15×65+0.3×75+0.25×85+0.05×95=71．…（6分）
第一、二、三组的频率之和为0.1+0.15+0.15=0.4
所以中位数=70+≈73.33…（8分）
（3）由频率分步直方图可得，成绩是40～50分的有40×0.1=4人，
90～100分的学生有40×0.05=2人，记取出的2个人的成绩为x，y，
“|x-y|>10”说明选出的2个人一个成绩在[40，50）内，
另一个在[50，60）内，
故满足“|x-y|>10”的选法有 4×2=8种，
而所有的取法有=15种，
故满足“|x-y|>10”的概率p=．…（14分）