“三等分角”是古希腊几何尺规作图当中的名题，和化圆为方、倍立方问题被并列为古代数学的三大难题之一，而如今数学上已证实这个问题无解，数学家普斯借助函数给出一种“三等分角”的方法．探究如图1，已知：矩形PQRM的顶点P、R都在函数y=1x（x>0）的图象上，试证明：点Q必在直线OM上；应用如图2，将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上，边OA与函数y=1x（x>0）的图象交于点P，以P为原心，以2OP位半径作弧交图象于点R，分别过点P和R作x轴，y轴的平行线，两直线交于点M、点Q，连
2019-04-12
“三等分角”是古希腊几何尺规作图当中的名题，和化圆为方、倍立方问题被并列为古代数学的三大难题之一，而如今数学上已证实这个问题无解，数学家普斯借助函数给出一种“三等分角”的方法．
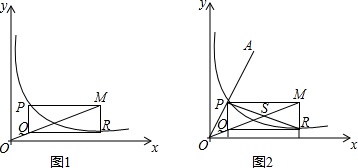
探究
如图1，已知：矩形PQRM的顶点P、R都在函数y=
（x>0）的图象上，试证明：点Q必在直线OM上；
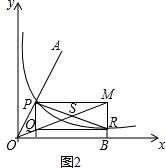
应用
如图2，将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上，边OA与函数y=
（x>0）的图象交于点P，以P为原心，以2OP位半径作弧交图象于点R，分别过点P和R作x轴，y轴的平行线，两直线交于点M、点Q，
连接OM，则∠MOB=
∠AOB，请你用所学的知识证明：∠MOB=
∠AOB．
探究
如图1，已知：矩形PQRM的顶点P、R都在函数y=
| 1 |
| x |
应用
如图2，将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上，边OA与函数y=
| 1 |
| x |
连接OM，则∠MOB=
| 1 |
| 3 |
| 1 |
| 3 |
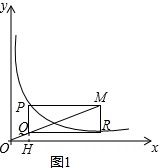（1）如图1，延长PQ交x轴于点H，设点P（a，