精选问答
某省物理学会为了研究高一学生物理成绩与性别的关系，选取了一次模拟考试中某班级的30名男生和20名女生的物理成绩，并整理得到如图所示的频率分布直方图，记80分以上（包含80分）为优秀，80分以下为非优秀．（Ⅰ）根据频率分布直方图，若按90%的可靠性要求，能否认为“成绩与性别有关系”？（Ⅱ）从本班物理成绩为优秀的学生中任取3人，记女生的人数为随机变量X，求X的分布列和数学期望．参考公式：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)参考数据：P（K2≥k0）0.100.050.0250.01

2019-05-28

某省物理学会为了研究高一学生物理成绩与性别的关系，选取了一次模拟考试中某班级的30名男生和20名女生的物理成绩，并整理得到如图所示的频率分布直方图，记80分以上（包含80分）为优秀，80分以下为非优秀．

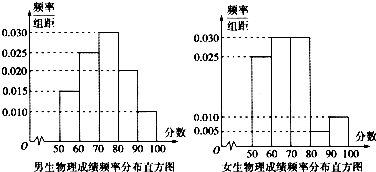
（Ⅰ）根据频率分布直方图，若按90%的可靠性要求，能否认为“成绩与性别有关系”？
（Ⅱ）从本班物理成绩为优秀的学生中任取3人，记女生的人数为随机变量X，求X的分布列和数学期望．
参考公式：K2=
n(ad−bc)2
(a+b)(c+d)(a+c)(b+d)

参考数据：
P（K2≥k0）0.100.050.0250.010
k02.7063.8415.0246.635
优质解答
（Ⅰ）男生中，优秀有0.3×30=9人，非优秀有21人，女生中，优秀有0.15×20=3人，非优秀有17人．
2×2列联表
优秀非优秀合计
男生92130
女生31720
合计123850
K2=
50×(9×17−3×21)2
30×20×12×38
≈1.48＜2.706
∴按90%的可靠性要求，不能认为“成绩与性别有关系”；
（Ⅱ）本班共有优秀12人，其中男9人，女3人，X=0，1，2，3，则
P（X=0）=
C
3
9
C
3
12
=
21
55
；P（X=1）=
C
1
3
C
2
9
C
3
12
=
27
55
；P（X=2）=
C
2
3
C
1
9
C
3
12
=
27
220
；P（X=3）=
C
3
3
C
3
12
=
1
220
；
∴X的分布列
X0123
P
21
55
27
55
27
220
1
220
数学期望EX=0×
21
55
+1×
27
55
+2×
27
220
+3×
1
220
=优秀非优秀合计男生92130女生31720合计123850K2=
50×(9×17−3×21)2
30×20×12×38
≈1.48＜2.706
∴按90%的可靠性要求，不能认为“成绩与性别有关系”；
（Ⅱ）本班共有优秀12人，其中男9人，女3人，X=0，1，2，3，则
P（X=0）=
C
3
9
C
3
12
=
21
55
；P（X=1）=
C
1
3
C
2
9
C
3
12
=
27
55
；P（X=2）=
C
2
3
C
1
9
C
3
12
=
27
220
；P（X=3）=
C
3
3
C
3
12
=
1
220
；
∴X的分布列
X0123
P
21
55
27
55
27
220
1
220
数学期望EX=0×
21
55
+1×
27
55
+2×
27
220
+3×
1
220
=
相关问答