优质解答
1.参看振幅的定义——“振动物体离开平衡位置的最大距离叫振动的振幅”
那么,距离有必要探讨正负吗?没有,那么,振幅没有负的说法.仅仅是指距离而已.
所以说,学物理最关键的是要弄清各种概念以及这些概念在物理学重要达到的作用.
2.劲度系数的物理意义是——在产生单位变形时提供的弹力的大小,由此可见,他描述的是弹簧之类弹性物体对抗变形的能力.
所以,把一个弹簧截断一半的话,他的劲度系数会变为原来的两倍.
原因如下:
长L的弹簧受力时,产生相应的变形S.这个S是由长L的多个环状钢丝共同形成的.
而截断一半时,L/2长的弹簧受到同样外力的情况下,只需要原来一半的变形就可以产生同样大小的弹力.
这样说不理解的话,我们进行逆向思考——考虑这样一个问题——
劲度系数完全相同的两根等长弹簧A和B,都受到同样大小的外拉力F,他们将产生一样的形变Sa和Sb.——这一点可以认同吧?
那么,把两根弹簧连接起来,我们把链接后的弹簧称作C吧,依然施加原来的外力,拉力F,先进行受力分析——
两根弹簧内部的弹力处处相等都为F.这一点没有问题吧?
那么下面我们探讨对于弹簧发生了什么事.
那么A受到的外力为F,会产生与他独立受力时同样的Sa的形变量,B也一样,会产生Sb的形变量,那么已经连接了AB的弹簧C来说,整体形变量是多少呢?
很自然,整体形变Sc是两个弹簧A和B形变量的和,即:
“Sc=Sa+Sb.”
又因为A和B两根弹簧完全一样,那么"Sa=Sb"
那么“Sc=2Sa=2Sb”.
所以我们有这样的结论——
两根同样的弹簧被连接起来的话,施加同样的外力,整体会产生原来单独受力时两倍的形变量.
在这一结论基础之上,参见劲度系数的定义与本质物理意义,我们得出下面的结论——
两根劲度系数为K的弹簧连接成新的弹簧时,抵抗外力的能力会变弱,劲度系数会变为原来的一半,即K~=K/2.
既然加长弹簧会使得劲度系数减小,那么,相反的,揭短弹簧会使劲度系数增大.
这里最关键的有两点:
第一,对于弹簧或者绳子之类提供弹力的物理模型,它们提供力的方式是付出变形的代价.因为形变是整体效果,所以说他们内部的弹力是处处相等的.
第二,要认识到弹簧的形变实际上是无数小形变的累加效果,弹簧越长这种累加效果越显著.
在清楚弹簧型变得来源之后,我建议楼主考虑这样的问题——
1.弹簧有没有“并联”与“串联”的规律可循?
2.多根弹簧串 并联会产生什么样的变化?有无规律可循呢?
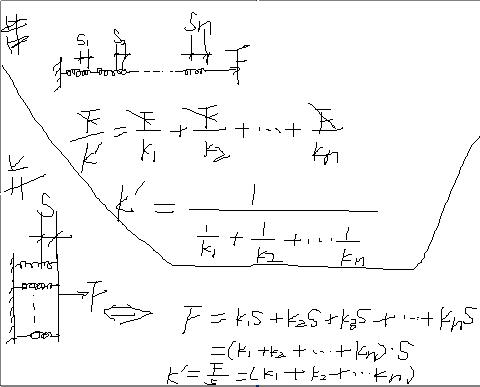
经总结,得出结论如下——我会附图给出推算过程.
1.N根弹簧串联时,最终形成的新弹簧的劲度系数为参与串联的各个弹簧劲度系数的“倒数和的倒数”.
2.N根弹簧并联时,形成的新弹簧的劲度系数为参与并联的各个弹簧劲度系数的和.
推导过程见图——
 1.参看振幅的定义——“振动物体离开平衡位置的最大距离叫振动的振幅”
1.参看振幅的定义——“振动物体离开平衡位置的最大距离叫振动的振幅”
那么,距离有必要探讨正负吗?没有,那么,振幅没有负的说法.仅仅是指距离而已.
所以说,学物理最关键的是要弄清各种概念以及这些概念在物理学重要达到的作用.
2.劲度系数的物理意义是——在产生单位变形时提供的弹力的大小,由此可见,他描述的是弹簧之类弹性物体对抗变形的能力.
所以,把一个弹簧截断一半的话,他的劲度系数会变为原来的两倍.
原因如下:
长L的弹簧受力时,产生相应的变形S.这个S是由长L的多个环状钢丝共同形成的.
而截断一半时,L/2长的弹簧受到同样外力的情况下,只需要原来一半的变形就可以产生同样大小的弹力.
这样说不理解的话,我们进行逆向思考——考虑这样一个问题——
劲度系数完全相同的两根等长弹簧A和B,都受到同样大小的外拉力F,他们将产生一样的形变Sa和Sb.——这一点可以认同吧?
那么,把两根弹簧连接起来,我们把链接后的弹簧称作C吧,依然施加原来的外力,拉力F,先进行受力分析——
两根弹簧内部的弹力处处相等都为F.这一点没有问题吧?
那么下面我们探讨对于弹簧发生了什么事.
那么A受到的外力为F,会产生与他独立受力时同样的Sa的形变量,B也一样,会产生Sb的形变量,那么已经连接了AB的弹簧C来说,整体形变量是多少呢?
很自然,整体形变Sc是两个弹簧A和B形变量的和,即:
“Sc=Sa+Sb.”
又因为A和B两根弹簧完全一样,那么"Sa=Sb"
那么“Sc=2Sa=2Sb”.
所以我们有这样的结论——
两根同样的弹簧被连接起来的话,施加同样的外力,整体会产生原来单独受力时两倍的形变量.
在这一结论基础之上,参见劲度系数的定义与本质物理意义,我们得出下面的结论——
两根劲度系数为K的弹簧连接成新的弹簧时,抵抗外力的能力会变弱,劲度系数会变为原来的一半,即K~=K/2.
既然加长弹簧会使得劲度系数减小,那么,相反的,揭短弹簧会使劲度系数增大.
这里最关键的有两点:
第一,对于弹簧或者绳子之类提供弹力的物理模型,它们提供力的方式是付出变形的代价.因为形变是整体效果,所以说他们内部的弹力是处处相等的.
第二,要认识到弹簧的形变实际上是无数小形变的累加效果,弹簧越长这种累加效果越显著.
在清楚弹簧型变得来源之后,我建议楼主考虑这样的问题——
1.弹簧有没有“并联”与“串联”的规律可循?
2.多根弹簧串 并联会产生什么样的变化?有无规律可循呢?
经总结,得出结论如下——我会附图给出推算过程.
1.N根弹簧串联时,最终形成的新弹簧的劲度系数为参与串联的各个弹簧劲度系数的“倒数和的倒数”.
2.N根弹簧并联时,形成的新弹簧的劲度系数为参与并联的各个弹簧劲度系数的和.
推导过程见图——

那么,距离有必要探讨正负吗?没有,那么,振幅没有负的说法.仅仅是指距离而已.
所以说,学物理最关键的是要弄清各种概念以及这些概念在物理学重要达到的作用.
2.劲度系数的物理意义是——在产生单位变形时提供的弹力的大小,由此可见,他描述的是弹簧之类弹性物体对抗变形的能力.
所以,把一个弹簧截断一半的话,他的劲度系数会变为原来的两倍.
原因如下:
长L的弹簧受力时,产生相应的变形S.这个S是由长L的多个环状钢丝共同形成的.
而截断一半时,L/2长的弹簧受到同样外力的情况下,只需要原来一半的变形就可以产生同样大小的弹力.
这样说不理解的话,我们进行逆向思考——考虑这样一个问题——
劲度系数完全相同的两根等长弹簧A和B,都受到同样大小的外拉力F,他们将产生一样的形变Sa和Sb.——这一点可以认同吧?
那么,把两根弹簧连接起来,我们把链接后的弹簧称作C吧,依然施加原来的外力,拉力F,先进行受力分析——
两根弹簧内部的弹力处处相等都为F.这一点没有问题吧?
那么下面我们探讨对于弹簧发生了什么事.
那么A受到的外力为F,会产生与他独立受力时同样的Sa的形变量,B也一样,会产生Sb的形变量,那么已经连接了AB的弹簧C来说,整体形变量是多少呢?
很自然,整体形变Sc是两个弹簧A和B形变量的和,即:
“Sc=Sa+Sb.”
又因为A和B两根弹簧完全一样,那么"Sa=Sb"
那么“Sc=2Sa=2Sb”.
所以我们有这样的结论——
两根同样的弹簧被连接起来的话,施加同样的外力,整体会产生原来单独受力时两倍的形变量.
在这一结论基础之上,参见劲度系数的定义与本质物理意义,我们得出下面的结论——
两根劲度系数为K的弹簧连接成新的弹簧时,抵抗外力的能力会变弱,劲度系数会变为原来的一半,即K~=K/2.
既然加长弹簧会使得劲度系数减小,那么,相反的,揭短弹簧会使劲度系数增大.
这里最关键的有两点:
第一,对于弹簧或者绳子之类提供弹力的物理模型,它们提供力的方式是付出变形的代价.因为形变是整体效果,所以说他们内部的弹力是处处相等的.
第二,要认识到弹簧的形变实际上是无数小形变的累加效果,弹簧越长这种累加效果越显著.
在清楚弹簧型变得来源之后,我建议楼主考虑这样的问题——
1.弹簧有没有“并联”与“串联”的规律可循?
2.多根弹簧串 并联会产生什么样的变化?有无规律可循呢?
经总结,得出结论如下——我会附图给出推算过程.
1.N根弹簧串联时,最终形成的新弹簧的劲度系数为参与串联的各个弹簧劲度系数的“倒数和的倒数”.
2.N根弹簧并联时,形成的新弹簧的劲度系数为参与并联的各个弹簧劲度系数的和.
推导过程见图——
 1.参看振幅的定义——“振动物体离开平衡位置的最大距离叫振动的振幅”
1.参看振幅的定义——“振动物体离开平衡位置的最大距离叫振动的振幅”那么,距离有必要探讨正负吗?没有,那么,振幅没有负的说法.仅仅是指距离而已.
所以说,学物理最关键的是要弄清各种概念以及这些概念在物理学重要达到的作用.
2.劲度系数的物理意义是——在产生单位变形时提供的弹力的大小,由此可见,他描述的是弹簧之类弹性物体对抗变形的能力.
所以,把一个弹簧截断一半的话,他的劲度系数会变为原来的两倍.
原因如下:
长L的弹簧受力时,产生相应的变形S.这个S是由长L的多个环状钢丝共同形成的.
而截断一半时,L/2长的弹簧受到同样外力的情况下,只需要原来一半的变形就可以产生同样大小的弹力.
这样说不理解的话,我们进行逆向思考——考虑这样一个问题——
劲度系数完全相同的两根等长弹簧A和B,都受到同样大小的外拉力F,他们将产生一样的形变Sa和Sb.——这一点可以认同吧?
那么,把两根弹簧连接起来,我们把链接后的弹簧称作C吧,依然施加原来的外力,拉力F,先进行受力分析——
两根弹簧内部的弹力处处相等都为F.这一点没有问题吧?
那么下面我们探讨对于弹簧发生了什么事.
那么A受到的外力为F,会产生与他独立受力时同样的Sa的形变量,B也一样,会产生Sb的形变量,那么已经连接了AB的弹簧C来说,整体形变量是多少呢?
很自然,整体形变Sc是两个弹簧A和B形变量的和,即:
“Sc=Sa+Sb.”
又因为A和B两根弹簧完全一样,那么"Sa=Sb"
那么“Sc=2Sa=2Sb”.
所以我们有这样的结论——
两根同样的弹簧被连接起来的话,施加同样的外力,整体会产生原来单独受力时两倍的形变量.
在这一结论基础之上,参见劲度系数的定义与本质物理意义,我们得出下面的结论——
两根劲度系数为K的弹簧连接成新的弹簧时,抵抗外力的能力会变弱,劲度系数会变为原来的一半,即K~=K/2.
既然加长弹簧会使得劲度系数减小,那么,相反的,揭短弹簧会使劲度系数增大.
这里最关键的有两点:
第一,对于弹簧或者绳子之类提供弹力的物理模型,它们提供力的方式是付出变形的代价.因为形变是整体效果,所以说他们内部的弹力是处处相等的.
第二,要认识到弹簧的形变实际上是无数小形变的累加效果,弹簧越长这种累加效果越显著.
在清楚弹簧型变得来源之后,我建议楼主考虑这样的问题——
1.弹簧有没有“并联”与“串联”的规律可循?
2.多根弹簧串 并联会产生什么样的变化?有无规律可循呢?
经总结,得出结论如下——我会附图给出推算过程.
1.N根弹簧串联时,最终形成的新弹簧的劲度系数为参与串联的各个弹簧劲度系数的“倒数和的倒数”.
2.N根弹簧并联时,形成的新弹簧的劲度系数为参与并联的各个弹簧劲度系数的和.
推导过程见图——
