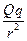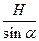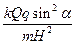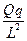静电场与引力场有着非常相似的性质,力的形式都遵从平方反比定律,解答下列问题:(1)写出万有引力定律和库仑定律中的常数G与K的单位。(2)某星球的质量为M,在该星球表面某一倾角为θ的山坡上以初速度v 0 平抛一个物体,经 时间该物体落到山坡上。欲使该物体不再落回该星球的表面,至少应以多大的速度抛出物体(不计一切阻力,万有引力常量为G)?(3)如图所示,质量为 m 的小球A穿在绝缘细杆上,杆的倾角为α,小球A带正电,电量为 q ,在杆上B点处固定一个电量为 Q 的正电荷。将A由距B竖直高度为 H 处无初速释
2019-06-26
| 静电场与引力场有着非常相似的性质,力的形式都遵从平方反比定律,解答下列问题: (1)写出万有引力定律和库仑定律中的常数G与K的单位。 (2)某星球的质量为M,在该星球表面某一倾角为θ的山坡上以初速度v 0 平抛一个物体,经 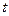 时间该物体落到山坡上。欲使该物体不再落回该星球的表面,至少应以多大的速度抛出物体(不计一切阻力,万有引力常量为G)? 时间该物体落到山坡上。欲使该物体不再落回该星球的表面,至少应以多大的速度抛出物体(不计一切阻力,万有引力常量为G)?(3)如图所示,质量为 m 的小球A穿在绝缘细杆上,杆的倾角为α,小球A带正电,电量为 q ,在杆上B点处固定一个电量为 Q 的正电荷。将A由距B竖直高度为 H 处无初速释放,小球A下滑过程中电量不变。不计A与细杆间的摩擦,整个装置处在真空中。已知静电力恒量 k 和重力加速度 g ,求:A球刚释放时的加速度以及当A球的动能最大时,A球与B点的距离。 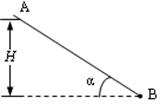 |
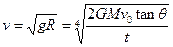 (3)
(3)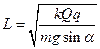
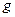 ,由平抛运动可得
,由平抛运动可得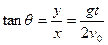 ① 故
① 故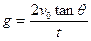
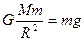 ②所以
②所以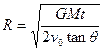
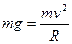 ③
③