为了调查某校2000名高中生的体能情况,从中随机选取m名学生进行体能测试,将得到的成绩分成[60,70),[70,80),…,[110,120]六个组,并作出如下频率分布直方图,已知第四组的频数为12,图中从左到右的第一、二个矩形的面积比为4:5.规定:成绩在[60,70)、[70,90)、[90,110)、[110,120)的分别记为“不合格”、“合格”、“良好”,“优秀”,根据图中的信息,回答下列问题. (Ⅰ)求x和m的值,并补全这个频率分布直方图;(Ⅱ)利用样本估计总体的思想,估计该校学生体能情况为
2019-11-22
为了调查某校2000名高中生的体能情况,从中随机选取m名学生进行体能测试,将得到的成绩分成[60,70),[70,80),…,[110,120]六个组,并作出如下频率分布直方图,已知第四组的频数为12,图中从左到右的第一、二个矩形的面积比为4:5.规定:成绩在[60,70)、[70,90)、[90,110)、[110,120)的分别记为“不合格”、“合格”、“良好”,“优秀”,根据图中的信息,回答下列问题.
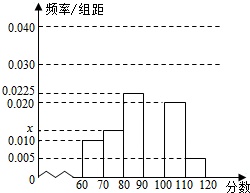
(Ⅰ)求x和m的值,并补全这个频率分布直方图;
(Ⅱ)利用样本估计总体的思想,估计该校学生体能情况为“优秀或良好”的人数;
(Ⅲ)根据频率分布直方图,从“不合格”和“优秀”的两组学生中随机抽取2人,求所抽取的2人恰好形成“一帮一”(一个优秀、一个不合格)互助小组的概率.
优质解答
 (本题满分12分)
(本题满分12分)
(Ⅰ)依题意得:=,…(1分)
解得x=0.0125…(2分)
∴第四组的频率为1-10(0.010+0.0125+0.0225+0.020+0.005)=0.3,…(3分)
∴=0.3,解得m=40…(4分)
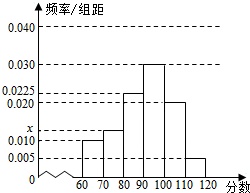
补全频率分布直方图如图…(5分)
(Ⅱ)由图估计“优秀或良好”的人数为2000×10×(0.03+0.02+0.005)(6分)=1100(7分)
(Ⅲ)“不合格”的人数为0.010×10×40=4,
“优秀”的人数为0.005×10×40=2,(8分)
设“不合格”的4人分别为a1,a2,a3,a4,“优秀”的2人分别为b1,b2,
从中任取2人的所有基本事件为:
(a1,a2),(a1,a3),(a1,a4),(a1,b1),(a1,b2),(a2,a3),
(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),
(a4,b1),(a4,b2),(b1,b2),共15种(10分)
设所抽取的2人恰好形成“一帮一”互助小组为事件A,其中包含的基本事件为:
(a1,b1),(a1,b2),(a2,b1),(a2,b2),
(a3,b1),(a3,b2),(a4,b1),(a4,b2),共有8种,(11分)
故所抽取的2人恰好形成“一帮一”互助小组的概率P(A)=.(12分)
(注:15种基本事件,全对得(2分),列错1~7种扣(1分),错8种及以上不给分)
 (本题满分12分)
(本题满分12分)
(Ⅰ)依题意得:=,…(1分)
解得x=0.0125…(2分)
∴第四组的频率为1-10(0.010+0.0125+0.0225+0.020+0.005)=0.3,…(3分)
∴=0.3,解得m=40…(4分)
补全频率分布直方图如图…(5分)
(Ⅱ)由图估计“优秀或良好”的人数为2000×10×(0.03+0.02+0.005)(6分)=1100(7分)
(Ⅲ)“不合格”的人数为0.010×10×40=4,
“优秀”的人数为0.005×10×40=2,(8分)
设“不合格”的4人分别为a1,a2,a3,a4,“优秀”的2人分别为b1,b2,
从中任取2人的所有基本事件为:
(a1,a2),(a1,a3),(a1,a4),(a1,b1),(a1,b2),(a2,a3),
(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),
(a4,b1),(a4,b2),(b1,b2),共15种(10分)
设所抽取的2人恰好形成“一帮一”互助小组为事件A,其中包含的基本事件为:
(a1,b1),(a1,b2),(a2,b1),(a2,b2),
(a3,b1),(a3,b2),(a4,b1),(a4,b2),共有8种,(11分)
故所抽取的2人恰好形成“一帮一”互助小组的概率P(A)=.(12分)
(注:15种基本事件,全对得(2分),列错1~7种扣(1分),错8种及以上不给分)


 (本题满分12分)
(本题满分12分)