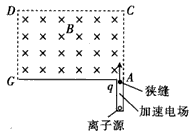
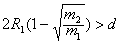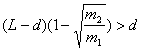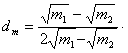利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用。如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场,A处有一狭缝。离子源产生的离子,经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场,运动到GA边,被相应的收集器收集。整个装置内部为真空,已知被加速的两种正离子的质量分别是m 1 和m 2 (m 1 >m 2 ),电荷量均为q。加速电场的电势差为U,离子进入电场时的初速度可以忽略。不计重力,也不考虑离子间的相互作用。(1)求质量
2019-04-14
| 利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用。如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场,A处有一狭缝。离子源产生的离子,经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场,运动到GA边,被相应的收集器收集。整个装置内部为真空,已知被加速的两种正离子的质量分别是m 1 和m 2 (m 1 >m 2 ),电荷量均为q。加速电场的电势差为U,离子进入电场时的初速度可以忽略。不计重力,也不考虑离子间的相互作用。 (1)求质量为m 1 的离子进入磁场时的速率V 1 。 (2)当磁感应强度的大小为B时,求两种离子在GA边落点的间距s。 (3)在前面的讨论中忽略了狭缝宽度的影响,实际装置中狭缝具有一定宽度。若狭缝过宽,可能使两束离子在GA边上的落点区域交叠,导致两种离子无法完全分离,设磁感应强度大小可调,GA边长为定值L,狭缝宽度为d,狭缝右边缘在A处,离子可以从狭缝各处射入磁场,入射方向仍垂直于GA边且垂直于磁场。为保证上述两种离子能落在GA边上并被完全分离,求狭缝的最大宽度。 |
 |
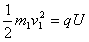
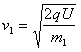 ①
①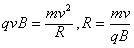
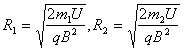 ②
② ③
③