| 数列 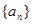 ,满足 ,满足 (1)求 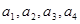 ,并猜想通项公式 ,并猜想通项公式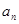 。 。(2)用数学归纳法证明(1)中的猜想。 |
| (1) 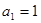 , ,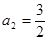 , ,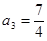 , ,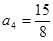 并猜想通项公式 并猜想通项公式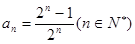 。(2)见解析 。(2)见解析 |
| 本试题主要考查了数列的通项公式求解,并用数学归纳法加以证明。第一问利用递推关系式得到 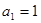 , ,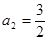 , ,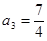 , ,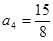 ,并猜想通项公式 ,并猜想通项公式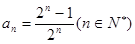 第二问中,用数学归纳法证明(1)中的猜想。 ①对n=1, 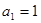 等式成立。 等式成立。②假设n=k 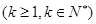 时, 时,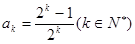 成立, 成立,那么当n=k+1时, 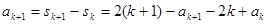 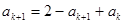 ,所以当n=k+1时结论成立可证。 ,所以当n=k+1时结论成立可证。数列 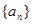 ,满足 ,满足 (1) 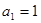 , ,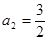 , ,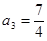 , ,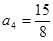 并猜想通项公 并猜想通项公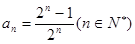 。 …4分 。 …4分(2)用数学归纳法证明(1)中的猜想。①对n=1, 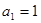 等式成立。 …5分 等式成立。 …5分②假设n=k 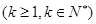 时, 时,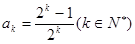 成立, 成立,那么当n=k+1时, 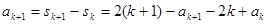 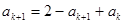 , ……9分 , ……9分所以 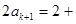 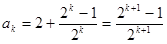 所以当n=k+1时结论成立 ……11分 由①②知,猜想对一切自然数n 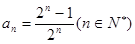 均成立 均成立 |
| 数列 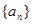 ,满足 ,满足 (1)求 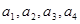 ,并猜想通项公式 ,并猜想通项公式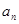 。 。(2)用数学归纳法证明(1)中的猜想。 |
| (1) 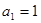 , ,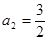 , ,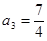 , ,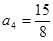 并猜想通项公式 并猜想通项公式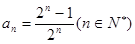 。(2)见解析 。(2)见解析 |
| 本试题主要考查了数列的通项公式求解,并用数学归纳法加以证明。第一问利用递推关系式得到 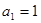 , ,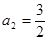 , ,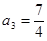 , ,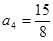 ,并猜想通项公式 ,并猜想通项公式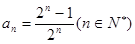 第二问中,用数学归纳法证明(1)中的猜想。 ①对n=1, 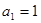 等式成立。 等式成立。②假设n=k 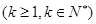 时, 时,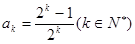 成立, 成立,那么当n=k+1时, 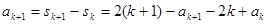 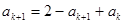 ,所以当n=k+1时结论成立可证。 ,所以当n=k+1时结论成立可证。数列 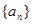 ,满足 ,满足 (1) 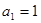 , ,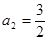 , ,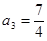 , ,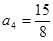 并猜想通项公 并猜想通项公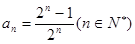 。 …4分 。 …4分(2)用数学归纳法证明(1)中的猜想。①对n=1, 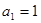 等式成立。 …5分 等式成立。 …5分②假设n=k 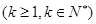 时, 时,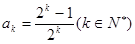 成立, 成立,那么当n=k+1时, 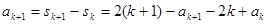 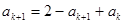 , ……9分 , ……9分所以 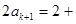 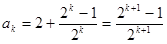 所以当n=k+1时结论成立 ……11分 由①②知,猜想对一切自然数n 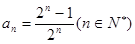 均成立 均成立 |