数学
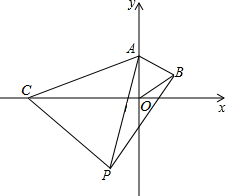（2014•淄博）如图，在直角坐标系中，点A的坐标是（0，3），点C是x轴上的一个动点，点C在x轴上移动时，始终保持△ACP是等边三角形．当点C移动到点O时，得到等边三角形AOB（此时点P与点B重合）．（1）点C在移动的过程中，当等边三角形ACP的顶点P在第三象限时（如图），求证：△AOC≌△ABP；由此你发现什么结论？（2）求点C在x轴上移动时，点P所在函数图象的解析式．

2019-04-29

（2014•淄博）如图，在直角坐标系中，点A的坐标是（0，3），点C是x轴上的一个动点，点C在x轴上移动时，始终保持△ACP是等边三角形．当点C移动到点O时，得到等边三角形AOB（此时点P与点B重合）．
（1）点C在移动的过程中，当等边三角形ACP的顶点P在第三象限时（如图），求证：△AOC≌△ABP；由此你发现什么结论？
（2）求点C在x轴上移动时，点P所在函数图象的解析式．
优质解答
（1）证明：∵△AOB与△ACP都是等边三角形，
∴AO=AB，AC=AP，∠CAP=∠OAB=60°，
∴∠CAP+∠PAO=∠OAB+∠PAO，
∴∠CAO=∠PAB，
在△AOC与△ABP中，
AO＝AB
∠CAO＝∠PAB
AC＝AP

∴△AOC≌△ABP（SAS）．
∴∠COA=∠PBA=90°，
∴点P在过点B且与AB垂直的直线上或PB⊥AB或∠ABP=90°．
故结论是：点P在过点B且与AB垂直的直线上或PB⊥AB或∠ABP=90°；

（2）点P在过点B且与AB垂直的直线上．
∵△AOB是等边三角形，A（0，3），
∴B（
3
3
2
，
3
2
）．
当点C移动到点P在y轴上时，得P（0，-3）．
设点P所在的直线方程为：y=kx+b（k≠0）．把点B、P的坐标分别代入，得
3
3
2
k+b＝
3
2
b＝−3
，
解得
AO＝AB
∠CAO＝∠PAB
AC＝AP

∴△AOC≌△ABP（SAS）．
∴∠COA=∠PBA=90°，
∴点P在过点B且与AB垂直的直线上或PB⊥AB或∠ABP=90°．
故结论是：点P在过点B且与AB垂直的直线上或PB⊥AB或∠ABP=90°；

（2）点P在过点B且与AB垂直的直线上．
∵△AOB是等边三角形，A（0，3），
∴B（
3
3
2
，
3
2
）．
当点C移动到点P在y轴上时，得P（0，-3）．
设点P所在的直线方程为：y=kx+b（k≠0）．把点B、P的坐标分别代入，得
3
3
2
k+b＝
3
2
b＝−3
，
解得
相关问答