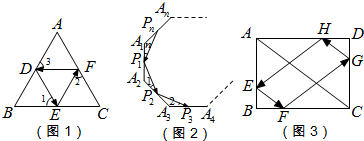
我们在初中物理已经学了光的反射定律:①入射光线、反射光线、法线都在同一个平面上;②入射光线、反射光线分居于法线两侧; ③入射角等于反射角.请你利用这一定律及初中数学知识解决以下问题:(1)如图1,在等边△ABC中,点D、E、F分别是其三边的中点,一条光线由点D出发,经DE→EF→FD反射回到D点,则图1中∠1+∠2+∠3=;(2)如图2,在正n边形A1A2A3…An中,点P1、P2、P3…Pn分别是正n边形各边上的中点,一条光线从P1点出发,经点P2、P3…Pn反射回到点P1,则图2中∠A2P2P1=(用
2019-05-22
我们在初中物理已经学了光的反射定律:①入射光线、反射光线、法线都在同一个平面上;②入射光线、反射光线分居于法线两侧; ③入射角等于反射角.请你利用这一定律及初中数学知识解决以下问题:
(1)如图1,在等边△ABC中,点D、E、F分别是其三边的中点,一条光线由点D出发,经DE→EF→FD反射回到D点,则图1中∠1+∠2+∠3=___;
(2)如图2,在正n边形A1A2A3…An中,点P1、P2、P3…Pn分别是正n边形各边上的中点,一条光线从P1点出发,经点P2、P3…Pn反射回到点P1,则图2中∠A2P2P1=___(用含n的代数式表示);
(3)如图3,在矩形ABCD,若AB=3,BC=4,点E是AB上的动点(不与A、B重合),一条光线从点E出发,入射光线EF与对角线AC平行,经BC、CD、AD上的点F、G、H反射回到E点,得四边形EFGH.
①求tan∠AHE的值;
②问:四边形EFGH的周长是否为定值?若是,请求出该值;若不是,请说明理由.
优质解答
(1)如图1,∵△ABC为等边三角形,点D、E、F分别是其三边的中点,
∴∠B=∠C=∠A=60°,BD=BE=EC=CF=AF=AD,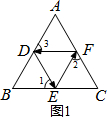
∴△BDE,△CEF,△ADF均为等边三角形,
∴∠1=∠2=∠3=60°
∴∠1+∠2+∠3=180°,
故答案为:180°;
(2)如图2,由(1)的结论可得:∠1+∠2+∠3+…∠n=180°,
∴∠A2P2P1=,
故答案为:
(3)如图3,
方法一:①连结AC交EH,FG于点J,K,
∵EF∥AC
∴∠BEF=∠BAC,
由入射角等于反射角的结论得:∠BEF=∠AEH,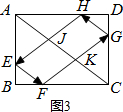
∴∠AEH=∠BAC
∴tan∠AEH=∠tan∠BAC=;
②∵∠AEH=∠BAC,
∴AJ=EJ,
∵∠AEH+∠AHE=90°,∠EAC+∠ACB=90°,∠AEH=∠EAC,
∴∠AHE=∠ACB,
又∵AD∥BC,
∴∠ACB=∠CAD,
∴∠CAD=∠AHE,
∴AJ=HJ,
同理FK=KC,GK=KC,EF=JK,HG=JK,
∴LEFGH=HE+EF+FG+GH=2AJ+2KC+2JK=2AC=10,
∴四边形EFGH的周长为定值10;
方法二:①如图4,依据题意得∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8,
∵EF∥AC,
∴∠1=∠ACB,∠8=∠BAC,
∴∠7=∠BAC即∠AEH=∠BAC,
∴tan∠AEH=tan∠BAC==;
②∵四边形ABCD是矩形,
∴∠CAD=∠AC,
又∵EF∥AC,
∴∠1=∠ACB,
∴∠1=∠CAD,
而∠1=∠2,∠3=∠4,且∠2+∠3=90°,
∴∠1+∠4=90°,
又∠4+∠5=90°,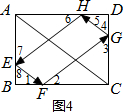
∴∠5=∠1,
∴∠5=∠CAD,
∴GH∥AC,
∴EF∥GH,
在Rt△EBF,Rt△FCG和Rt△GDH中,
设BE=3x,则BF=4x,EF=5x,
∴FC=4-4x,CG=CF=3-3x,
∴DG=3=CG=3x,
∴BE=DG=3x,
又∵∠5=∠1,
∴△EBF≌△GDH,
∴EF=GH,
∴四边形EFGH是平行四边形,
又∵FG==5-5x,
∴四边形EFGH的周长为2(EF+FG)=2(5x+5-5x)=10,
∴四边形EFGH的周长为定值10.
(1)如图1,∵△ABC为等边三角形,点D、E、F分别是其三边的中点,
∴∠B=∠C=∠A=60°,BD=BE=EC=CF=AF=AD,
∴△BDE,△CEF,△ADF均为等边三角形,
∴∠1=∠2=∠3=60°
∴∠1+∠2+∠3=180°,
故答案为:180°;
(2)如图2,由(1)的结论可得:∠1+∠2+∠3+…∠n=180°,
∴∠A2P2P1=,
故答案为:
(3)如图3,
方法一:①连结AC交EH,FG于点J,K,
∵EF∥AC
∴∠BEF=∠BAC,
由入射角等于反射角的结论得:∠BEF=∠AEH,
∴∠AEH=∠BAC
∴tan∠AEH=∠tan∠BAC=;
②∵∠AEH=∠BAC,
∴AJ=EJ,
∵∠AEH+∠AHE=90°,∠EAC+∠ACB=90°,∠AEH=∠EAC,
∴∠AHE=∠ACB,
又∵AD∥BC,
∴∠ACB=∠CAD,
∴∠CAD=∠AHE,
∴AJ=HJ,
同理FK=KC,GK=KC,EF=JK,HG=JK,
∴LEFGH=HE+EF+FG+GH=2AJ+2KC+2JK=2AC=10,
∴四边形EFGH的周长为定值10;
方法二:①如图4,依据题意得∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8,
∵EF∥AC,
∴∠1=∠ACB,∠8=∠BAC,
∴∠7=∠BAC即∠AEH=∠BAC,
∴tan∠AEH=tan∠BAC==;
②∵四边形ABCD是矩形,
∴∠CAD=∠AC,
又∵EF∥AC,
∴∠1=∠ACB,
∴∠1=∠CAD,
而∠1=∠2,∠3=∠4,且∠2+∠3=90°,
∴∠1+∠4=90°,
又∠4+∠5=90°,
∴∠5=∠1,
∴∠5=∠CAD,
∴GH∥AC,
∴EF∥GH,
在Rt△EBF,Rt△FCG和Rt△GDH中,
设BE=3x,则BF=4x,EF=5x,
∴FC=4-4x,CG=CF=3-3x,
∴DG=3=CG=3x,
∴BE=DG=3x,
又∵∠5=∠1,
∴△EBF≌△GDH,
∴EF=GH,
∴四边形EFGH是平行四边形,
又∵FG==5-5x,
∴四边形EFGH的周长为2(EF+FG)=2(5x+5-5x)=10,
∴四边形EFGH的周长为定值10.





