当n∈N*时,,(Ⅰ)求S1,S2,T1,T2;(Ⅱ)猜想Sn与Tn的关系,并用数学归纳法证明.
2019-04-14
当n∈N*时,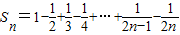 ,
,
(Ⅰ)求S1,S2,T1,T2;
(Ⅱ)猜想Sn与Tn的关系,并用数学归纳法证明.
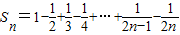 ,
,(Ⅰ)求S1,S2,T1,T2;
(Ⅱ)猜想Sn与Tn的关系,并用数学归纳法证明.
2019-04-14
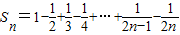 ,
,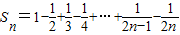 ,Tn=
,Tn=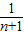 +
+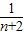 +
+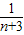 +…+
+…+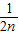 .
. =
= ,S2=1-
,S2=1- +
+ -
- =
=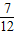 ,T1=
,T1=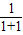 =
= ,T2=
,T2=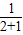 +
+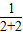 =
=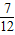 (2分)
(2分) +
+ -
- +…+
+…+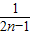 -
- =
=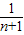 +
+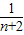 +
+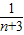 +…+
+…+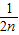
 +
+ -
- +…+
+…+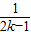 -
-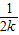 =
=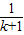 +
+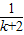 +
+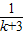 +…+
+…+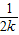 (8分)
(8分) -
-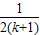 =Tk+
=Tk+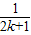 -
-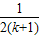 (10分)
(10分)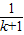 +
+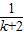 +
+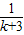 +…+
+…+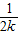 +
+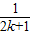 -
-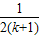 (11分)
(11分)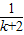 +
+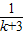 +…+
+…+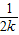 +
+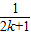 +(
+(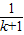 -
-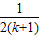 )
)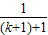 +
+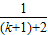 +…+
+…+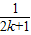 +
+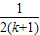 =Tk+1,
=Tk+1,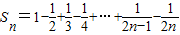 ,Tn=
,Tn=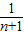 +
+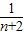 +
+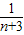 +…+
+…+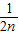 .
. =
= ,S2=1-
,S2=1- +
+ -
- =
=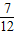 ,T1=
,T1=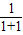 =
= ,T2=
,T2=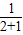 +
+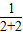 =
=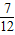 (2分)
(2分) +
+ -
- +…+
+…+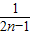 -
- =
=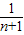 +
+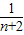 +
+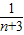 +…+
+…+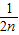
 +
+ -
- +…+
+…+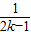 -
-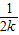 =
=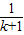 +
+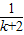 +
+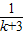 +…+
+…+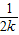 (8分)
(8分) -
-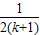 =Tk+
=Tk+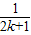 -
-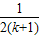 (10分)
(10分)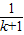 +
+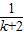 +
+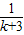 +…+
+…+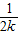 +
+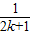 -
-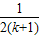 (11分)
(11分)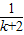 +
+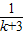 +…+
+…+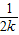 +
+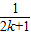 +(
+(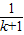 -
-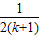 )
)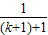 +
+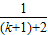 +…+
+…+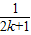 +
+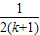 =Tk+1,
=Tk+1,