数学活动--求重叠部分的面积.问题情境:数学活动课上,老师出示了一个问题:如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
2019-04-14
数学活动--求重叠部分的面积.
问题情境:数学活动课上,老师出示了一个问题:
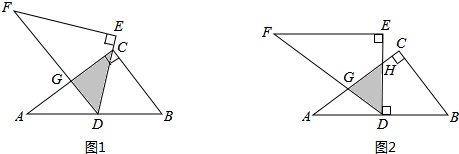
如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
优质解答
(1)∵∠ACB=90°,D是AB的中点,
∴DC=DB=DA.
∴∠B=∠DCB.
又∵△ABC≌△FDE,
∴∠FDE=∠B.
∴∠FDE=∠DCB.
∴DG∥BC.
∴∠AGD=∠ACB=90°.
∴DG⊥AC.
又∵DC=DA,
∴G是AC的中点.
∴CG=AC=×8=4,DG=BC=×6=3.
∴S△DCG=×CG•DG=×4×3=6.
(2)如图2所示:
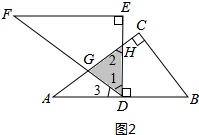 ∵△ABC≌△FDE,
∵△ABC≌△FDE,
∴∠B=∠1.
∵∠C=90°,ED⊥AB,
∴∠A+∠B=90°,∠A+∠2=90°,
∴∠B=∠2,
∴∠1=∠2,
∴GH=GD,
∵∠A+∠2=90°,∠1+∠3=90°,
∴∠A=∠3,
∴AG=GD,
∴AG=GH,
∴点G为AH的中点;
在Rt△ABC中,AB===10,
∵D是AB中点,
∴AD=AB=5,
在△ADH与△ACB中,∵∠A=∠A,∠ADH=∠ACB=90°,
∴△ADH∽△ACB,
∴=,
∴=,
∴DH=.
∴S△DGH=S△ADH=××DH•AD=××5=.
(1)∵∠ACB=90°,D是AB的中点,
∴DC=DB=DA.
∴∠B=∠DCB.
又∵△ABC≌△FDE,
∴∠FDE=∠B.
∴∠FDE=∠DCB.
∴DG∥BC.
∴∠AGD=∠ACB=90°.
∴DG⊥AC.
又∵DC=DA,
∴G是AC的中点.
∴CG=AC=×8=4,DG=BC=×6=3.
∴S△DCG=×CG•DG=×4×3=6.
(2)如图2所示:
 ∵△ABC≌△FDE,
∵△ABC≌△FDE,
∴∠B=∠1.
∵∠C=90°,ED⊥AB,
∴∠A+∠B=90°,∠A+∠2=90°,
∴∠B=∠2,
∴∠1=∠2,
∴GH=GD,
∵∠A+∠2=90°,∠1+∠3=90°,
∴∠A=∠3,
∴AG=GD,
∴AG=GH,
∴点G为AH的中点;
在Rt△ABC中,AB===10,
∵D是AB中点,
∴AD=AB=5,
在△ADH与△ACB中,∵∠A=∠A,∠ADH=∠ACB=90°,
∴△ADH∽△ACB,
∴=,
∴=,
∴DH=.
∴S△DGH=S△ADH=××DH•AD=××5=.
相关问答
- 求解一道数学题(请用通俗易懂的方法解释)张
- 六年级数学应用题(动脑筋)1.用一张正方形
- 把6本数学书和4本语文书放到书架上面,指定
- 6本中文书和4本外语书任意往书架上摆放,则
- 数学应用题(等比数列)某制糖厂第一年制糖5
- 小学三年级数学口算题目,最起码一千道
- 看看这数学题红红兰兰一起集邮,红红的张数占
- 若有数学书4本,语文书两本,若数学书要排在
- 100张100元的新版人民币大约0.9厘米
- 高中数学 排列组合 5男4女排1排,(1)
- 一道关于乌龟爬行的数学题有一个正方形的房间
- 二年级上册数学2条6米长的皮筋绑在一起,接
- 还是一道小学4年纪的数学题,一副三角板中,
- 初三数学概率问题十个人带着十个不同帽子,将
- 数学求导对一连串的函数套在一起应如何求导,
- 小学数学三年级乘法和除法要一起复习吗


 ∵△ABC≌△FDE,
∵△ABC≌△FDE,