本题是一道压轴题,考查的知识众多,涉及到函数,数列,不等式,利用的方法有分析法与综合法等,综合性很强,难度较大.答案看这里http://gz.qiujieda.com/exercise/math/804256构造函数，等价转化是关键

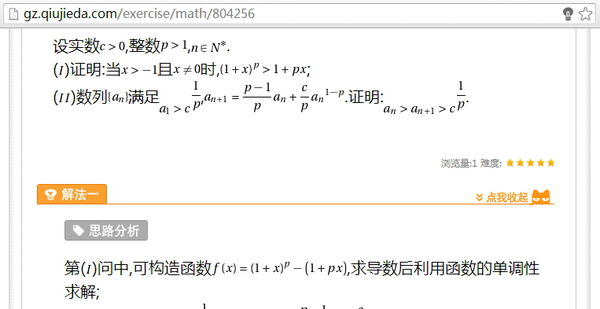
设实数c>0,整数p>1,n∈N*
证明:当x>-1且x不等于 0时，(1+x)^p>1+px
数列{an}满足a1>c^(1/p)，an+1=(p-1)an/p+ c*[an^(1-p)]/p。证明an>an+1>c^(1/p)

本题是一道压轴题,考查的知识众多,涉及到函数,数列,不等式,利用的方法有分析法与综合法等,综合性很强,难度较大.答案看这里http://gz.qiujieda.com/exercise/math/804256构造函数，等价转化是关键

设实数c>0,整数p>1,n∈N*
证明:当x>-1且x不等于 0时，(1+x)^p>1+px
数列{an}满足a1>c^(1/p)，an+1=(p-1)an/p+ c*[an^(1-p)]/p。证明an>an+1>c^(1/p)