（2012•珠海）某学校课程安排中，各班每天下午只安排三节课．（1）初一（1）班星期二下午安排了数学、英语、生物课各一节，通过画树状图求出把数学课安排在最后一节的概率；（2）星期三下午，初二（1）班安排了数学、物理、政治课各一节，初二（2）班安排了数学、语文、地理课各一节，此时两班这六节课的每一种课表排法出现的概率是136．已知这两个班的数学课都有同一个老师担任，其他课由另外四位老师担任．求这两个班数学课不相冲突的概率（直接写结果）．
2019-04-15
（2012•珠海）某学校课程安排中，各班每天下午只安排三节课．
（1）初一（1）班星期二下午安排了数学、英语、生物课各一节，通过画树状图求出把数学课安排在最后一节的概率；
（2）星期三下午，初二（1）班安排了数学、物理、政治课各一节，初二（2）班安排了数学、语文、地理课各一节，此时两班这六节课的每一种课表排法出现的概率是．已知这两个班的数学课都有同一个老师担任，其他课由另外四位老师担任．求这两个班数学课不相冲突的概率（直接写结果）．
优质解答
（1）如图，共有6种情况，
数学科安排在最后一节的概率是=；
（2）如图，两个班级的课程安排，（1）班的每一种安排可以与（2）班的所有安排情况相对应，
所有共有6×6=36种情况，
每一种组合都有6种情况，其中有2种情况数学课冲突，其余4种情况不冲突，
所有，不冲突的情况有4×6=24，
数学课不相冲突的概率为：=．
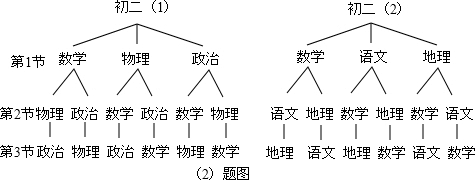（1）如图，共有6种情况，
数学科安排在最后一节的概率是=；
（2）如图，两个班级的课程安排，（1）班的每一种安排可以与（2）班的所有安排情况相对应，
所有共有6×6=36种情况，
每一种组合都有6种情况，其中有2种情况数学课冲突，其余4种情况不冲突，
所有，不冲突的情况有4×6=24，
数学课不相冲突的概率为：=．