（2010•淄博二模）如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AA1=BC=2AC=2．（Ⅰ）若D为AA1中点，求证：平面B1CD⊥平面B1C1D；（Ⅱ）在AA1上是否存在一点D，使得二面角B1-CD-C1的大小为60°．
2019-04-29
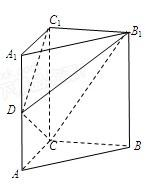（2010•淄博二模）如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AA1=BC=2AC=2．
（Ⅰ）若D为AA1中点，求证：平面B1CD⊥平面B1C1D；
（Ⅱ）在AA1上是否存在一点D，使得二面角B1-CD-C1的大小为60°．
优质解答
解法一：（Ⅰ）证明：∵∠A1C1B1=∠ACB=90°
∴B1C1⊥A1C1
又由直三棱柱性质知B1C1⊥CC1（1分）∴B1C1⊥平面ACC1A1．
∴B1C1⊥CD（2分）
由AA1=BC=2AC=2，D为AA1中点，可知DC＝DC1＝，
∴DC2+DC12=CC12=4即CD⊥DC1（4分）
又B1C1⊥CD∴CD⊥平面B1C1D
又CD⊂平面B1CD
故平面B1CD⊥平面B1C1D（6分）
（Ⅱ）当AD＝AA1时二面角B1-CD-C1的大小为60°．（7分）
假设在AA1上存在一点D满足题意，
由（Ⅰ）可知B1C1⊥平面ACC1A1．
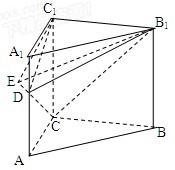
如图，在平面ACC1A1内过C1作C1E⊥CD，交CD或延长线或于E，连EB1，则EB1⊥CD
所以∠B1EC1为二面角B1-CD-C1的平面角（8分）
∴∠B1EC1=60°
由B1C1=2知，C1E＝（10分）
设AD=x，则DC＝
∵△DCC1的面积为1∴•＝1
解得
解法一：（Ⅰ）证明：∵∠A1C1B1=∠ACB=90°
∴B1C1⊥A1C1
又由直三棱柱性质知B1C1⊥CC1（1分）∴B1C1⊥平面ACC1A1．
∴B1C1⊥CD（2分）
由AA1=BC=2AC=2，D为AA1中点，可知DC＝DC1＝，
∴DC2+DC12=CC12=4即CD⊥DC1（4分）
又B1C1⊥CD∴CD⊥平面B1C1D
又CD⊂平面B1CD
故平面B1CD⊥平面B1C1D（6分）
（Ⅱ）当AD＝AA1时二面角B1-CD-C1的大小为60°．（7分）
假设在AA1上存在一点D满足题意，
由（Ⅰ）可知B1C1⊥平面ACC1A1．
如图，在平面ACC1A1内过C1作C1E⊥CD，交CD或延长线或于E，连EB1，则EB1⊥CD
所以∠B1EC1为二面角B1-CD-C1的平面角（8分）
∴∠B1EC1=60°
由B1C1=2知，C1E＝（10分）
设AD=x，则DC＝
∵△DCC1的面积为1∴•＝1
解得