优质解答
已知：如图；直线a∥b∥c，直线AC、DF被直线a、b、c所截，交点分别为A、B、C、D、E、F，AB=BC，
求证：DE=EF
证明：过点A作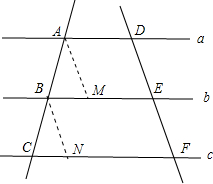
AM∥DE，交b于点M，作BN∥EF，交c于点N，
∵a∥b∥c，
∴四边形AMED、四边形BNFE是平行四边形，
∴AM=DE，BN=EF，
∵AM∥DN，
∴∠BAM=∠CBN，
∵c∥b，
∴∠ABM=∠BCN，
在△ABM和△BCN中，
，
∴△ABM≌△BCN，
∴AM=BN，
∴DE=EF． 已知：如图；直线a∥b∥c，直线AC、DF被直线a、b、c所截，交点分别为A、B、C、D、E、F，AB=BC，
求证：DE=EF
证明：过点A作AM∥DE，交b于点M，作BN∥EF，交c于点N，
∵a∥b∥c，
∴四边形AMED、四边形BNFE是平行四边形，
∴AM=DE，BN=EF，
∵AM∥DN，
∴∠BAM=∠CBN，
∵c∥b，
∴∠ABM=∠BCN，
在△ABM和△BCN中，
，
∴△ABM≌△BCN，
∴AM=BN，
∴DE=EF．
求证：DE=EF
证明：过点A作
AM∥DE，交b于点M，作BN∥EF，交c于点N，∵a∥b∥c，
∴四边形AMED、四边形BNFE是平行四边形，
∴AM=DE，BN=EF，
∵AM∥DN，
∴∠BAM=∠CBN，
∵c∥b，
∴∠ABM=∠BCN，
在△ABM和△BCN中，
|
∴△ABM≌△BCN，
∴AM=BN，
∴DE=EF． 已知：如图；直线a∥b∥c，直线AC、DF被直线a、b、c所截，交点分别为A、B、C、D、E、F，AB=BC，
求证：DE=EF
证明：过点A作
AM∥DE，交b于点M，作BN∥EF，交c于点N，∵a∥b∥c，
∴四边形AMED、四边形BNFE是平行四边形，
∴AM=DE，BN=EF，
∵AM∥DN，
∴∠BAM=∠CBN，
∵c∥b，
∴∠ABM=∠BCN，
在△ABM和△BCN中，
|
∴△ABM≌△BCN，
∴AM=BN，
∴DE=EF．