如图,已知抛物线经过A(4,0),B(2,3),C(0,3)三点. (1)求抛物线的解析式及对称轴. (2)在抛物线的对称轴上找一点M,使得MA+MB的值最小,并求出点M的坐标. (3)在抛物线上是否存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
2019-05-07
如图,已知抛物线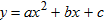 经过A(4,0),B(2,3),C(0,3)三点.
经过A(4,0),B(2,3),C(0,3)三点.
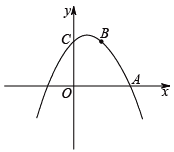
(1)求抛物线的解析式及对称轴.
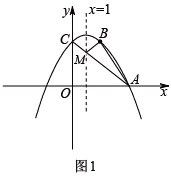
(2)在抛物线的对称轴上找一点M,使得MA+MB的值最小,并求出点M的坐标.
(3)在抛物线上是否存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.____
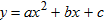 经过A(4,0),B(2,3),C(0,3)三点.
经过A(4,0),B(2,3),C(0,3)三点.
(1)求抛物线的解析式及对称轴.
(2)在抛物线的对称轴上找一点M,使得MA+MB的值最小,并求出点M的坐标.
(3)在抛物线上是否存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.____
 ,求得此抛物线的对称轴;
,求得此抛物线的对称轴; 经过A(4,0)、B(2,3)、C(0,3)三点,得
经过A(4,0)、B(2,3)、C(0,3)三点,得

 ;
; .
.


 .
.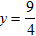 .
.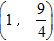 .
.
 ,则BC∥A
,则BC∥A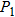 .
. .
.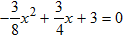 .
.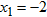 ,
, .
. (-2,0).
(-2,0). ,BC=2,
,BC=2, ≠BC,
≠BC, 为梯形;
为梯形; ∥AB,交抛物线于点
∥AB,交抛物线于点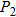 .
. 与x轴交于点N,
与x轴交于点N,

 .
. 既在直线CN:
既在直线CN: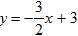 上,又在抛物线:
上,又在抛物线: 上,
上, .
. .
. (舍去),
(舍去), .
. 横坐标为6,
横坐标为6, x+3,当x=6时,y=-6.
x+3,当x=6时,y=-6. (6,-6).
(6,-6). ≠CN,
≠CN, ≠AB,
≠AB, 为梯形.
为梯形.