（2014•宿迁模拟）如图所示，在xoy平面内有一范围足够大的匀强电场，电场强度大小为E，电场方向在图中未画出．在y≤l的区域内有磁感应强度为B的匀强磁场，磁场方向垂直于xoy平面向里．一电荷量为+q、质量为m的粒子，从O点由静止释放，运动到磁场边界P点时的速度刚好为零，P点坐标为（l，l），不计粒子所受重力．（1）求从O点到P点的过程中电场力对带电粒子做的功，并判断匀强电场的方向；（2）若该粒子在O点以沿OP方向、大小v0=E2B的初速度开始运动，并从P点离开磁场，此过程中运动到离过OP的直线最远位置的
2019-06-26
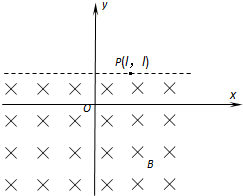（2014•宿迁模拟）如图所示，在xoy平面内有一范围足够大的匀强电场，电场强度大小为E，电场方向在图中未画出．在y≤l的区域内有磁感应强度为B的匀强磁场，磁场方向垂直于xoy平面向里．一电荷量为+q、质量为m的粒子，从O点由静止释放，运动到磁场边界P点时的速度刚好为零，P点坐标为（l，l），不计粒子所受重力．
（1）求从O点到P点的过程中电场力对带电粒子做的功，并判断匀强电场的方向；
（2）若该粒子在O点以沿OP方向、大小v0=的初速度开始运动，并从P点离开磁场，此过程中运动到离过OP的直线最远位置的加速度大小a=，则此点离OP直线的距离是多少？
（3）若有另一电荷量为-q、质量为m的粒子能从O点匀速穿出磁场，设l=，求该粒子离开磁场后到达y轴时的位置坐标．
优质解答
（1）根据动能定理，从O到P过程中电场力对带电粒子做功：W=△E=0
直线OP是等势线，带电粒子能在复合场中运动到P点，则电场方向应为斜向右下与x轴正方向成45°
（2）磁场中运动到离直线OP最远位置时，速度方向平行于OP．洛伦兹力方向垂直于OP，设此位置粒子速度为v、离OP直线的距离为d，则：qvB-qE=ma
qEd＝mv2−mv02，
解得 v＝，d=；
（3）设粒子做匀速直线运动速度为v1，则qv1B=qE，
设粒子离开P点后在电场中做类平抛运动的加速度为a′，设从P点运动到y轴的过程中，粒子在OP方向的位移大小为x，则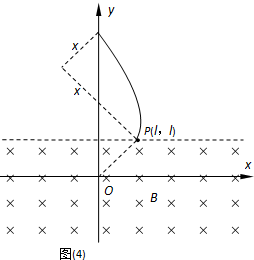
l+x＝a′t2，
qE=ma′
x=v1t，
解得x＝，
粒子通过y轴时的纵坐标为：
y＝2l+x＝．（或写成y=4l）．
答：（1）从O点到P点的过程中电场力对带电粒子做的功为0，电场方向应为斜向右下与x轴正方向成45°．
（2）此点离OP直线的距离是d=；
（3）该粒子离开磁场后到达y轴时的位置坐标
（1）根据动能定理，从O到P过程中电场力对带电粒子做功：W=△E=0
直线OP是等势线，带电粒子能在复合场中运动到P点，则电场方向应为斜向右下与x轴正方向成45°
（2）磁场中运动到离直线OP最远位置时，速度方向平行于OP．洛伦兹力方向垂直于OP，设此位置粒子速度为v、离OP直线的距离为d，则：qvB-qE=ma
qEd＝mv2−mv02，
解得 v＝，d=；
（3）设粒子做匀速直线运动速度为v1，则qv1B=qE，
设粒子离开P点后在电场中做类平抛运动的加速度为a′，设从P点运动到y轴的过程中，粒子在OP方向的位移大小为x，则
l+x＝a′t2，
qE=ma′
x=v1t，
解得x＝，
粒子通过y轴时的纵坐标为：
y＝2l+x＝．（或写成y=4l）．
答：（1）从O点到P点的过程中电场力对带电粒子做的功为0，电场方向应为斜向右下与x轴正方向成45°．
（2）此点离OP直线的距离是d=；
（3）该粒子离开磁场后到达y轴时的位置坐标