我们知道,由平行线可得出“同位角相等”,“内错角相等”等结论,因此,在几何证明中,我们往往可以通过添加平行线得到一些相等的角.(1)如图a,点D在△ABC边BC的延长线上,请你猜想∠ACD与∠A、∠B之间的数量关系,并请你在图中通过添加平行线的方法,证明你的猜想.猜想结论是证明:(2)如图b,四边形ABCD为一个凹四边形,请你利用(1)中你猜想的结论,求证:∠BDC=∠A+∠B+∠C;(3)如图c,已知BE平分∠ABD,CF平分∠ACD,BE与CF相交于点P,当∠BDC=130°,∠BAC=60°时,求∠
2019-06-01
我们知道,由平行线可得出“同位角相等”,“内错角相等”等结论,因此,在几何证明中,我们往往可以通过添加平行线得到一些相等的角.
(1)如图a,点D在△ABC边BC的延长线上,请你猜想∠ACD与∠A、∠B之间的数量关系,并请你在图中通过添加平行线的方法,证明你的猜想.猜想结论是______证明:
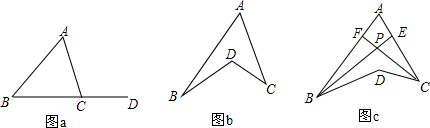
(2)如图b,四边形ABCD为一个凹四边形,请你利用(1)中你猜想的结论,求证:∠BDC=∠A+∠B+∠C;
(3)如图c,已知BE平分∠ABD,CF平分∠ACD,BE与CF相交于点P,当∠BDC=130°,∠BAC=60°时,求∠EPC的度数.
(1)如图a,点D在△ABC边BC的延长线上,请你猜想∠ACD与∠A、∠B之间的数量关系,并请你在图中通过添加平行线的方法,证明你的猜想.猜想结论是______证明:

(2)如图b,四边形ABCD为一个凹四边形,请你利用(1)中你猜想的结论,求证:∠BDC=∠A+∠B+∠C;
(3)如图c,已知BE平分∠ABD,CF平分∠ACD,BE与CF相交于点P,当∠BDC=130°,∠BAC=60°时,求∠EPC的度数.
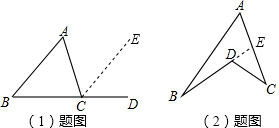 如图,过点C作CE∥AB,
如图,过点C作CE∥AB,