物理
（2012•广州二模）如图所示的水平地面，ab段粗糙，bc段光滑．可视为质点的物体A和B紧靠在一起，静止于b 处，已知A的质量为3m，B的质量为m．两物体在足够大的内力作用下突然沿水平方向左右分离，获得的总动能为E．B碰到c处的墙壁后等速率反弹，并追上已停在ab段的A．A、B与ab段的动摩擦因数均为μ，重力加速度为g．求：（1）分离瞬间A、B的速度大小；（2）A从分离到第一次停止的时间；（3）B第一次追上A时的速度大小．

2019-06-21

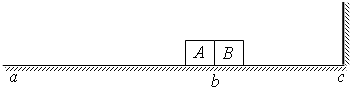
（2012•广州二模）如图所示的水平地面，ab段粗糙，bc段光滑．可视为质点的物体A和B紧靠在一起，静止于b 处，已知A的质量为3m，B的质量为m．两物体在足够大的内力作用下突然沿水平方向左右分离，获得的总动能为E．B碰到c处的墙壁后等速率反弹，并追上已停在ab段的A．A、B与ab段的动摩擦因数均为μ，重力加速度为g．求：

（1）分离瞬间A、B的速度大小；
（2）A从分离到第一次停止的时间；
（3）B第一次追上A时的速度大小．
优质解答
（1）物体A、B在内力作用下分离，设分离瞬间A速度大小为vA，B速度大小为vB，由A、B系统动量守恒定律有：
  3mvA=mvB …①
又由题意可知：E＝
1
2
•3m
v
2
A
+
1
2
•m
v
2
B
…②
联立①②可得：vA＝
E
6m
…③
vB＝
3E
2m
…④
（2）A、B分离后，A物体向左匀减速滑行，设滑行时间为tA，加速度大小为aA
对A应用牛顿第二定律：μ•3mg=3maA…⑤
得：a=μg  
A匀减速到停止的时间：tA＝
vA
aA
…⑥
联立③⑤⑥解得：tA＝
1
μg
E
6m
…⑦
（3）A、B分离后，A物体向左匀减速滑行，设滑行距离为sA
对A应用动能定理：−μ•3mgsA＝0−
1
2
•3m
v
2
A
…⑧
设B物体碰墙反弹后追上已停下的A物体时速度大小为v，
对B应用动能定理：−μmgsB＝
1
2
mv2−
1
2
m
v
2
B
…⑨
又因为B追上A时在粗糙面上滑行距离：sB=sA…⑩
联立解得：v＝
E＝
1
2
•3m
v
2
A
+
1
2
•m
v
2
B
…②
联立①②可得：vA＝
E
6m
…③
vB＝
3E
2m
…④
（2）A、B分离后，A物体向左匀减速滑行，设滑行时间为tA，加速度大小为aA
对A应用牛顿第二定律：μ•3mg=3maA…⑤
得：a=μg  
A匀减速到停止的时间：tA＝
vA
aA
…⑥
联立③⑤⑥解得：tA＝
1
μg
E
6m
…⑦
（3）A、B分离后，A物体向左匀减速滑行，设滑行距离为sA
对A应用动能定理：−μ•3mgsA＝0−
1
2
•3m
v
2
A
…⑧
设B物体碰墙反弹后追上已停下的A物体时速度大小为v，
对B应用动能定理：−μmgsB＝
1
2
mv2−
1
2
m
v
2
B
…⑨
又因为B追上A时在粗糙面上滑行距离：sB=sA…⑩
联立解得：v＝
相关问答