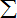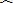已知某校5个学生的数学和物理成绩如下表: 学生的编号i 1 2 3 4 5 数学xi 80 75 70 65 60 物理yi 70 66 68 64 62(Ⅰ)通过大量事实证明发现,学生的数学成绩和物理成绩具有很强的线性相关关系,用x表示数学成绩,用y表示物理成绩,根据上述表格求y与x的回归方程;(Ⅱ)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?参考公式和数据:回
2019-04-02
已知某校5个学生的数学和物理成绩如下表:
(Ⅰ)通过大量事实证明发现,学生的数学成绩和物理成绩具有很强的线性相关关系,用x表示数学成绩,用y表示物理成绩,根据上述表格求y与x的回归方程;
(Ⅱ)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?
参考公式和数据:回归直线方程:
=bx+a,其中b=
,a=
−b
;
xiyi=23190,
=24750,残差和公式为:
(yi−
i).
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学xi | 80 | 75 | 70 | 65 | 60 |
| 物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?
参考公式和数据:回归直线方程:
| ̂ |
| y |
| |||||||
|
. |
| y |
. |
| x |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| x | 2 i |
| 5 |
 |
| i=1 |
| ̂ |
| y |