优质解答
| 程序框图如下:  |
| 算法分析:我们知道,若判别式Δ=b 2 -4ac>0,则原方程有两个不相等的实数根 x 1 = 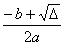 ,x 2 = ,x 2 = 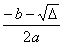 ; ;若Δ=0,则原方程有两个相等的实数根x 1 =x 2 = 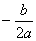 ; ;若Δ<0,则原方程没有实数根.也就是说,在求解方程之前,可以先判断判别式的符号,根据判断的结果执行不同的步骤,这个过程可以用条件结构实现. 又因为方程的两个根有相同的部分,为了避免重复计算,可以在计算x 1 和x 2 之前, 先计算p= 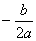 ,q= ,q= 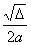 . .解决这一问题的算法步骤如下: 第一步,输入3个系数a,b,c. 第二步,计算Δ=b 2 -4ac. 第三步,判断Δ≥0是否成立.若是,则计算p= 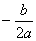 ,q= ,q= 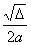 ;否则,输出“方程没有实数根”,结束算法. ;否则,输出“方程没有实数根”,结束算法.第四步,判断Δ=0是否成立.若是,则输出x 1 =x 2 =p;否则,计算x 1 =p+q,x 2 =p-q,并输出x 1 ,x 2 . |
| 程序框图如下:  |
| 算法分析:我们知道,若判别式Δ=b 2 -4ac>0,则原方程有两个不相等的实数根 x 1 = 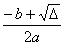 ,x 2 = ,x 2 = 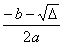 ; ;若Δ=0,则原方程有两个相等的实数根x 1 =x 2 = 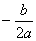 ; ;若Δ<0,则原方程没有实数根.也就是说,在求解方程之前,可以先判断判别式的符号,根据判断的结果执行不同的步骤,这个过程可以用条件结构实现. 又因为方程的两个根有相同的部分,为了避免重复计算,可以在计算x 1 和x 2 之前, 先计算p= 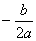 ,q= ,q= 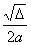 . .解决这一问题的算法步骤如下: 第一步,输入3个系数a,b,c. 第二步,计算Δ=b 2 -4ac. 第三步,判断Δ≥0是否成立.若是,则计算p= 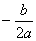 ,q= ,q= 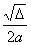 ;否则,输出“方程没有实数根”,结束算法. ;否则,输出“方程没有实数根”,结束算法.第四步,判断Δ=0是否成立.若是,则输出x 1 =x 2 =p;否则,计算x 1 =p+q,x 2 =p-q,并输出x 1 ,x 2 . |