如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷,电荷的质量为m、电量为q,不计电荷重力、电荷之间的作用力.(1)某电荷的运动轨迹和圆形区域的边缘交于P点,如图(甲)所示,∠POA=θ,求该电荷从A点出发时的速率.(2)若在圆形区域的边缘有一接收屏CBD,如图(乙)所示,C、D分别为接收屏上最边缘的两点,∠COB=∠BOD=30°
 如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷,电荷的质量为m、电量为q,不计电荷重力、电荷之间的作用力.
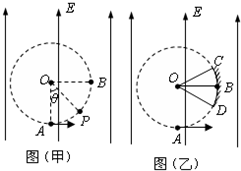
如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷,电荷的质量为m、电量为q,不计电荷重力、电荷之间的作用力.
(1)某电荷的运动轨迹和圆形区域的边缘交于P点,如图(甲)所示,∠POA=θ,求该电荷从A点出发时的速率.
(2)若在圆形区域的边缘有一接收屏CBD,如图(乙)所示,C、D分别为接收屏上最边缘的两点,∠COB=∠BOD=30°.求该屏上接收到的电荷的最大动能和最小动能.
2019-06-26
 如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷,电荷的质量为m、电量为q,不计电荷重力、电荷之间的作用力.
如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点.在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷,电荷的质量为m、电量为q,不计电荷重力、电荷之间的作用力.(1)某电荷的运动轨迹和圆形区域的边缘交于P点,如图(甲)所示,∠POA=θ,求该电荷从A点出发时的速率.
(2)若在圆形区域的边缘有一接收屏CBD,如图(乙)所示,C、D分别为接收屏上最边缘的两点,∠COB=∠BOD=30°.求该屏上接收到的电荷的最大动能和最小动能.