(2014•崇明县一模)根据三角形外心的概念,我们可引入下一个新定义:定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图,在Rt△ABC中,∠A=90°,BC=10,AB=6,如果准外心P在AC边上,那么PA的长为4或744或74.
 (2014•崇明县一模)根据三角形外心的概念,我们可引入下一个新定义:
(2014•崇明县一模)根据三角形外心的概念,我们可引入下一个新定义:
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
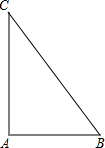
根据准外心的定义,探究如下问题:如图,在Rt△ABC中,∠A=90°,BC=10,AB=6,如果准外心P在AC边上,那么PA的长为
2019-06-02
 (2014•崇明县一模)根据三角形外心的概念,我们可引入下一个新定义:
(2014•崇明县一模)根据三角形外心的概念,我们可引入下一个新定义:定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
根据准外心的定义,探究如下问题:如图,在Rt△ABC中,∠A=90°,BC=10,AB=6,如果准外心P在AC边上,那么PA的长为
4或
| 7 |
| 4 |
4或
.
| 7 |
| 4 |
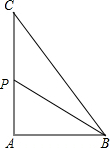 在Rt△ABC中,
在Rt△ABC中,