附加题(1)试用一元二次方程的求根公式,探索方程ax2+bx+c=0(a≠0)的两根互为相反数的条件是.(2)已知x、y为实数,3x-2+y2-4y+4=0,则xy=1313.(3)在直角梯形ABCD中,AD∥BC,∠C=90度,BC=16,AD=21,DC=12,动点P从点D出发,沿线段DA方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB以每秒1个单位长度的速度向点B运动.点P、Q分别从点D、C同时出发,当点P运动到点A时,点Q随之停止运动,设运动时间为t秒.①设△BPQ的面积为S,求S和
2019-05-27
 附加题
附加题
(1)试用一元二次方程的求根公式,探索方程ax2+bx+c=0(a≠0)的两根互为相反数的条件是______.
(2)已知x、y为实数,+y2-4y+4=0,则=.
(3)在直角梯形ABCD中,AD∥BC,∠C=90度,BC=16,AD=21,DC=12,动点P从点D出发,沿线段DA方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB以每秒1个单位长度的速度向点B运动.点P、Q分别从点D、C同时出发,当点P运动到点A时,点Q随之停止运动,设运动时间为t秒.
①设△BPQ的面积为S,求S和t之间的函数关系式;
②当t为何值时,以B、P、Q三点为顶点的三角形是等腰三等形?(分类讨论)
优质解答
(1)依题意可知:
x1+x2=−=0,
∵a≠0
∴b=0.
并且判别式△=b2-4ac≥0,则a,c异号.
故方程ax2+bx+c=0(a≠0)的两根互为相反数的条件是:b=0,且a,c异号.
(2)+y2−4y+4=0,
即+(y−2)2=0,
∴3x-2=0,y-2=0,
∴x=,y=2,
∴=.
(3)①作PM⊥BC,垂足为M.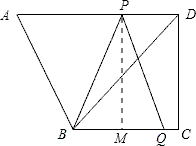
则四边形PDCM为矩形.
∴PM=DC=12
∵QB=16-t,
∴S=×12(16−t)=96−6t.
②可知CM=PD=2t,CQ=t,
若以B、P、Q三顶为顶点的三角形是等腰三角形,可以分三种情况:
第一种:PQ=BQ,在Rt△PMQ中,PQ2=PM2+QM2=122+t2,解t=.
第二种:BP=BQ,在Rt△PMB中,BP2=(16-2t)2+122,3t2-32t+144=0无实根,
∴PB≠BQ.
第三种:若PB=PQ,由PB2=PQ2得t2+122=(16-2t)2+122,解得t1=,t2=16(舍去)
综上可知:t=或t=,B、P、Q三点为顶点三角形是等腰三角形.
(1)依题意可知:
x1+x2=−=0,
∵a≠0
∴b=0.
并且判别式△=b2-4ac≥0,则a,c异号.
故方程ax2+bx+c=0(a≠0)的两根互为相反数的条件是:b=0,且a,c异号.
(2)+y2−4y+4=0,
即+(y−2)2=0,
∴3x-2=0,y-2=0,
∴x=,y=2,
∴=.
(3)①作PM⊥BC,垂足为M.
则四边形PDCM为矩形.
∴PM=DC=12
∵QB=16-t,
∴S=×12(16−t)=96−6t.
②可知CM=PD=2t,CQ=t,
若以B、P、Q三顶为顶点的三角形是等腰三角形,可以分三种情况:
第一种:PQ=BQ,在Rt△PMQ中,PQ2=PM2+QM2=122+t2,解t=.
第二种:BP=BQ,在Rt△PMB中,BP2=(16-2t)2+122,3t2-32t+144=0无实根,
∴PB≠BQ.
第三种:若PB=PQ,由PB2=PQ2得t2+122=(16-2t)2+122,解得t1=,t2=16(舍去)
综上可知:t=或t=,B、P、Q三点为顶点三角形是等腰三角形.
 附加题
附加题 附加题
附加题