宇航员乘坐宇宙飞船靠近某星球，首先在距离该星球球心r的圆轨道上观察星球表面，他发现宇宙飞船无动力绕星球的圆周运动周期为T；安全降落到星球表面后，他做了一个物理实验：如图所示，在倾角30°斜面上，以一定的初速度v0沿水平方向抛出一小物体，测得落点与抛出点的距离为L，根据以上描叙求解：（已知万有引力常量G）（1）该星球的质量为多少？（2）该星球的半径R为多大？
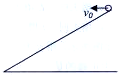宇航员乘坐宇宙飞船靠近某星球，首先在距离该星球球心r的圆轨道上观察星球表面，他发现宇宙飞船无动力绕星球的圆周运动周期为T；安全降落到星球表面后，他做了一个物理实验：如图所示，在倾角30°斜面上，以一定的初速度v0沿水平方向抛出一小物体，测得落点与抛出点的距离为L，根据以上描叙求解：（已知万有引力常量G）
（1）该星球的质量为多少？
（2）该星球的半径R为多大？
2019-05-27
宇航员乘坐宇宙飞船靠近某星球，首先在距离该星球球心r的圆轨道上观察星球表面，他发现宇宙飞船无动力绕星球的圆周运动周期为T；安全降落到星球表面后，他做了一个物理实验：如图所示，在倾角30°斜面上，以一定的初速度v0沿水平方向抛出一小物体，测得落点与抛出点的距离为L，根据以上描叙求解：（已知万有引力常量G）（1）该星球的质量为多少？
（2）该星球的半径R为多大？