(2010•佛山)一般来说,依据数学研究对象本质属性的相同点和差异点,将数学对象分为不同种类的数学思想叫做“分类”的思想;将事物进行分类,然后对划分的每一类分别进行研究和求解的方法叫做“分类讨论”的方法.请依据分类的思想和分类讨论的方法解决下列问题:如图,在△ABC中,∠ACB>∠ABC.(1)若∠BAC是锐角,请探索在直线AB上有多少个点D,能保证△ACD∽△ABC(不包括全等)?(2)请对∠BAC进行恰当的分类,直接写出每一类在直线AB上能保证△ACD∽△ABC(不包括全等)的点D的个数?
2019-04-27
(2010•佛山)一般来说,依据数学研究对象本质属性的相同点和差异点,将数学对象分为不同种类的数学思想叫做“分类”的思想;将事物进行分类,然后对划分的每一类分别进行研究和求解的方法叫做“分类讨论”的方法.请依 据分类的思想和分类讨论的方法解决下列问题:
据分类的思想和分类讨论的方法解决下列问题:
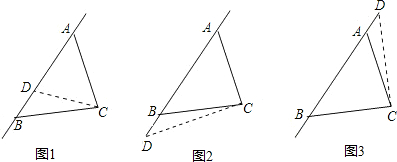
如图,在△ABC中,∠ACB>∠ABC.
(1)若∠BAC是锐角,请探索在直线AB上有多少个点D,能保证△ACD∽△ABC(不包括全等)?
(2)请对∠BAC进行恰当的分类,直接写出每一类在直线AB上能保证△ACD∽△ABC(不包括全等)的点D的个数?
 据分类的思想和分类讨论的方法解决下列问题:
据分类的思想和分类讨论的方法解决下列问题:如图,在△ABC中,∠ACB>∠ABC.
(1)若∠BAC是锐角,请探索在直线AB上有多少个点D,能保证△ACD∽△ABC(不包括全等)?
(2)请对∠BAC进行恰当的分类,直接写出每一类在直线AB上能保证△ACD∽△ABC(不包括全等)的点D的个数?