小明在做数学练习时,遇到下面的题目:题目:如图1,在△ABC中,D为AC边上一点,AB=AC,∠DBA=∠A,BD=BC.若CD=2,△BDC的周长为14,求AB的长.参考答案:AB=8.小明的计算结果与参考答案不同,因此他对参考答案产生了质疑.下面是他的分析、探究过程,请你补充完整.第一步,读题,并标记题目条件如下:在△ABC中,D为AC边上一点,①;②∠DBA=∠A;③;④;⑤.第二步,依据条件③、④、⑤,可以求得BD=BC=;第三步,作出△BCD,如图2所示;第四步,依据条件①,在图2中作出△ABC
2019-06-20
小明在做数学练习时,遇到下面的题目:
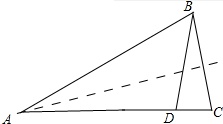
题目:如图1,在△ABC中,D为AC边上一点,AB=AC,∠DBA=∠A,BD=BC.若CD=2,△BDC的周长为14,求AB的长.
参考答案:AB=8.
小明的计算结果与参考答案不同,因此他对参考答案产生了质疑.下面是他的分析、探究过程,请你补充完整.
第一步,读题,并标记题目条件如下:
在△ABC中,D为AC边上一点,①___;②∠DBA=∠A;③___;④___;
⑤___.
第二步,依据条件③、④、⑤,可以求得BD=BC=___;
第三步,作出△BCD,如图2所示;
第四步,依据条件①,在图2中作出△ABC;(尺规作图,保留作图痕迹)
第五步,对所作图形进行观察、测量,发现与标记的条件___不符(填序号),去掉这个条件,题目中其他部分保持不变,求得AB的长为___.
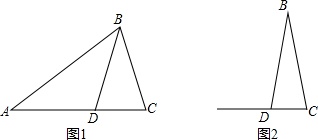
题目:如图1,在△ABC中,D为AC边上一点,AB=AC,∠DBA=∠A,BD=BC.若CD=2,△BDC的周长为14,求AB的长.
参考答案:AB=8.
小明的计算结果与参考答案不同,因此他对参考答案产生了质疑.下面是他的分析、探究过程,请你补充完整.
第一步,读题,并标记题目条件如下:
在△ABC中,D为AC边上一点,①___;②∠DBA=∠A;③___;④___;
⑤___.
第二步,依据条件③、④、⑤,可以求得BD=BC=___;
第三步,作出△BCD,如图2所示;
第四步,依据条件①,在图2中作出△ABC;(尺规作图,保留作图痕迹)
第五步,对所作图形进行观察、测量,发现与标记的条件___不符(填序号),去掉这个条件,题目中其他部分保持不变,求得AB的长为___.