精选问答
如图所示，在平行板电容器的两板之间，存在相互垂直的匀强磁场和匀强电场，磁感应强度B1=0.40T，方向垂直纸面向里，电场强度E=2.0×105V/m，方向竖直向下，PQ为板间中线．紧靠平行板右侧边缘xOy坐标系的第一象限内，有一垂直纸面的矩形匀强磁场区域，磁感应强度B2=0.25T．一束带电量q=8.0×10-19C、质量m=8.0×10-26 kg的正离子从P点射入平行板间，沿中线PQ做直线运动，穿出平行板后从y轴上坐标为（0，0.2m）的Q点垂直y轴射向磁场区，粒子飞出磁场区后从A点处穿过x

2019-06-26

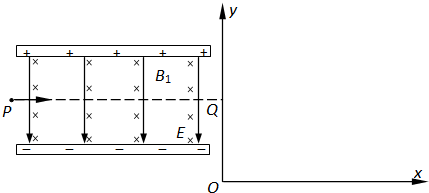
如图所示，在平行板电容器的两板之间，存在相互垂直的匀强磁场和匀强电场，磁感应强度B1=0.40T，方向垂直纸面向里，电场强度E=2.0×105V/m，方向竖直向下，PQ为板间中线．紧靠平行板右侧边缘xOy坐标系的第一象限内，有一垂直纸面的矩形匀强磁场区域，磁感应强度B2=0.25T．一束带电量q=8.0×10-19C、质量m=8.0×10-26 kg的正离子从P点射入平行板间，沿中线PQ做直线运动，穿出平行板后从y轴上坐标为（0，0.2m）的Q点垂直y轴射向磁场区，粒子飞出磁场区后从A点处穿过x轴，速度方向与x轴正向夹角为θ=60°，不计离子重力，求：

（1）离子运动的速度为多大？
（2）矩形磁场区的最小面积；
（3）粒子在矩形磁场中所经历的时间．
优质解答
（1）：离子在两板间时有：qE=qvB1
  解得：v=
E
B1
＝
2×105
0.4
m/s=5.0×105m/s   
（2）根据牛顿第二定律，由洛伦兹力提供向心力，则有：B2qv＝m
v2
r
，
解得：r=
mv
B2q
＝
8×10−26×5×105
0.5×8×10−19
m＝0.1m，
因从y轴上坐标为（0，0.2m）的Q点垂直y轴射向磁场区，所以离子做半圆后，从坐标原点射出回头．
因此矩形磁场区的最小面积为S=0.2×0.1m2=0.02m2；
（3）离子做圆周运动，周期公式T=
2πm
B2q
；
代入数据，解得：T=
2π×8×10−26
0.5×8×10−19
s
那么粒子在矩形磁场中所经历的时间为周期的一半，即为2π×10-7s；
答：（1）离子运动的速度为5.0×105m/s；
（2）矩形磁场区的最小面积为0.02m2；
（3）粒子在矩形磁场中所经历的时间为2π×10-7s． （1）：离子在两板间时有：qE=qvB1
  解得：v=
E
B1
＝
2×105
0.4
m/s=5.0×105m/s   
（2）根据牛顿第二定律，由洛伦兹力提供向心力，则有：B2qv＝m
v2
r
，
解得：r=
mv
B2q
＝
8×10−26×5×105
0.5×8×10−19
m＝0.1m，
因从y轴上坐标为（0，0.2m）的Q点垂直y轴射向磁场区，所以离子做半圆后，从坐标原点射出回头．
因此矩形磁场区的最小面积为S=0.2×0.1m2=0.02m2；
（3）离子做圆周运动，周期公式T=
2πm
B2q
；
代入数据，解得：T=
2π×8×10−26
0.5×8×10−19
s
那么粒子在矩形磁场中所经历的时间为周期的一半，即为2π×10-7s；
答：（1）离子运动的速度为5.0×105m/s；
（2）矩形磁场区的最小面积为0.02m2；
（3）粒子在矩形磁场中所经历的时间为2π×10-7s．
相关问答