数学
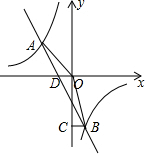
（2014•成都高新区一模）如图，在平面直角坐标系中，双曲线y=mx和直线y=kx+b交于A，B两点，点A的坐标为（-3，2），BC⊥y轴于点C，且OC=6BC．（1）求双曲线和直线的解析式；（2）求△AOB的面积．

2019-06-19

（2014•成都高新区一模）如图，在平面直角坐标系中，双曲线y=
m
x
和直线y=kx+b交于A，B两点，点A的坐标为（-3，2），BC⊥y轴于点C，且OC=6BC．
（1）求双曲线和直线的解析式；
（2）求△AOB的面积．
优质解答
（1）∵A（-3，2）在反比例y=
m
x
图象上，
∴m=-3×2=-6，
∴反比例函数解析式为y=-
6
x
；
∵BC⊥y轴于点C，且OC=6BC，
∴设B点坐标为（t，-6t）（t＞0），
把B（t，-6t）代入y=-
6
x
得t1=1，t2=-1（舍去），
∴B点坐标为（1，-6），
把A（-3，2）、B（1，-6）代入y=kx+b得
−3k+b＝2
k+b＝−6
，
解得
k＝−2
b＝−4
．
∴一次函数解析式为y=-2x-4；
（2）直线y=-2x-4交x轴于点D，如图，
把y=0代入y=-2x-4得-2x-4=0，解得x=-2，
则D点坐标为（-2，0），
△AOB的面积=S△AOD+S△BOD
=
1
2
×2×2+
1
2
×2×6
=8． （1）∵A（-3，2）在反比例y=
m
x
图象上，
∴m=-3×2=-6，
∴反比例函数解析式为y=-
6
x
；
∵BC⊥y轴于点C，且OC=6BC，
∴设B点坐标为（t，-6t）（t＞0），
把B（t，-6t）代入y=-
6
x
得t1=1，t2=-1（舍去），
∴B点坐标为（1，-6），
把A（-3，2）、B（1，-6）代入y=kx+b得
−3k+b＝2
k+b＝−6
，
解得
k＝−2
b＝−4
．
∴一次函数解析式为y=-2x-4；
（2）直线y=-2x-4交x轴于点D，如图，
把y=0代入y=-2x-4得-2x-4=0，解得x=-2，
则D点坐标为（-2，0），
△AOB的面积=S△AOD+S△BOD
=
1
2
×2×2+
1
2
×2×6
=8．
相关问答