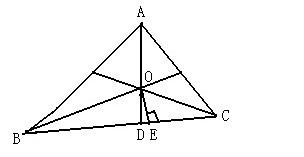
1、∵AD平分∠BAC

∴∠BAD＝∠BAC/2

∵BO平分∠ABC

∴∠ABO＝∠ABC/2

∴∠BOD＝∠BAD+∠ABO＝（∠BAC+∠ABC）/2＝（180°-∠ACB）/2＝90°-∠ACB/2

∵CO平分∠ACB

∴∠BCO＝∠ACB/2

∵OE⊥BC

∴∠COE+∠BCO＝90°

∴∠COE＝90°-∠BCO＝90°-∠ACB/2

∴∠BOD＝∠COE

2、AB平方=17平方=289

AC平方+BC平方=8平方+15平方=289

∴AB平方=AC平方+BC平方

∴△ABC是直角三角形,AC、BC是直角边

∵O是三角形内心

∴O到三边的距离相等=OE

∴S△ABC=S△AOB+S△AOC+S△BOC

                =1/2AB×OE+1/2AC×OE+1/2BC×OE

                =1/2OE(AB+AC+BC)

∵S△ABC=1/2AC×BC

∴OE=AC×BC/(ab+ac+bc)

       =8×15/(17+8+15)

       =3

1、∵AD平分∠BAC

∴∠BAD＝∠BAC/2

∵BO平分∠ABC

∴∠ABO＝∠ABC/2

∴∠BOD＝∠BAD+∠ABO＝（∠BAC+∠ABC）/2＝（180°-∠ACB）/2＝90°-∠ACB/2

∵CO平分∠ACB

∴∠BCO＝∠ACB/2

∵OE⊥BC

∴∠COE+∠BCO＝90°

∴∠COE＝90°-∠BCO＝90°-∠ACB/2

∴∠BOD＝∠COE

2、AB平方=17平方=289

AC平方+BC平方=8平方+15平方=289

∴AB平方=AC平方+BC平方

∴△ABC是直角三角形,AC、BC是直角边

∵O是三角形内心

∴O到三边的距离相等=OE

∴S△ABC=S△AOB+S△AOC+S△BOC

                =1/2AB×OE+1/2AC×OE+1/2BC×OE

                =1/2OE(AB+AC+BC)

∵S△ABC=1/2AC×BC

∴OE=AC×BC/(ab+ac+bc)

       =8×15/(17+8+15)

       =3