优质解答
【分析】(1)根据题意甲乙两人必须相邻的站法,把甲乙捆绑成一个整体与其余3人当着4个人作全排列有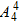 种,且甲、乙的位置还可以互换根据分步计数原理,得到结果;
种,且甲、乙的位置还可以互换根据分步计数原理,得到结果;
(2)除甲乙两人外其余3人的排列数为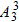 ,而甲乙二人应插其余3人排好的空才不相邻;且甲、乙位置可以互换.故有
,而甲乙二人应插其余3人排好的空才不相邻;且甲、乙位置可以互换.故有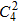
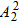 种排列方式;
种排列方式;
(3)若甲站最右端,则乙与其余三人可任意排,则此时的排法数为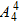 种;若甲不站最右端,则先从中间3个位置中选一个给甲,再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为
种;若甲不站最右端,则先从中间3个位置中选一个给甲,再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为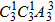 种;
种;
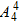 种,且甲、乙的位置还可以互换根据分步计数原理,得到结果;
种,且甲、乙的位置还可以互换根据分步计数原理,得到结果;(2)除甲乙两人外其余3人的排列数为
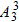 ,而甲乙二人应插其余3人排好的空才不相邻;且甲、乙位置可以互换.故有
,而甲乙二人应插其余3人排好的空才不相邻;且甲、乙位置可以互换.故有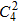
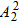 种排列方式;
种排列方式;(3)若甲站最右端,则乙与其余三人可任意排,则此时的排法数为
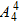 种;若甲不站最右端,则先从中间3个位置中选一个给甲,再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为
种;若甲不站最右端,则先从中间3个位置中选一个给甲,再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为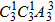 种;
种;(1)把甲乙捆绑成一个整体与其余3人当着4个人作全排列有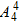 种,
种,
且甲、乙的位置还可以互换,
∴不同站法有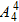
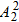 =48种.
=48种.
(2)除甲乙两人外其余3人的排列数为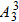 ,
,
而甲乙二人应插其余3人排好的空才不相邻;
且甲、乙位置可以互换.故有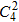
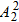 种排列方式.
种排列方式.
∴不同站法有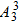 •
•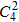
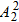 =72种.
=72种.
(3)优先考虑甲:
若甲站最右端,则乙与其余三人可任意排,则此时的排法数为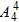 种;
种;
若甲不站最右端,则先从中间3个位置中选一个给甲,
再从除最右端的省余的3个位置给乙,其余的三个人任意排,
则此时的排法数为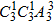 种;
种;
∴不同站法有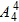 +
+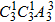 =78种.
=78种.
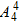 种,
种,且甲、乙的位置还可以互换,
∴不同站法有
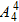
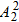 =48种.
=48种.(2)除甲乙两人外其余3人的排列数为
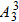 ,
,而甲乙二人应插其余3人排好的空才不相邻;
且甲、乙位置可以互换.故有
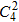
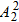 种排列方式.
种排列方式.∴不同站法有
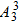 •
•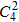
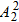 =72种.
=72种.(3)优先考虑甲:
若甲站最右端,则乙与其余三人可任意排,则此时的排法数为
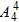 种;
种;若甲不站最右端,则先从中间3个位置中选一个给甲,
再从除最右端的省余的3个位置给乙,其余的三个人任意排,
则此时的排法数为
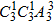 种;
种;∴不同站法有
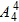 +
+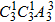 =78种.
=78种.【点评】本题考查排列组合的实际应用,是一个排列问题,注意相邻问题的排法,有限制条件的元素,要优先考虑.
【分析】(1)根据题意甲乙两人必须相邻的站法,把甲乙捆绑成一个整体与其余3人当着4个人作全排列有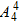 种,且甲、乙的位置还可以互换根据分步计数原理,得到结果;
种,且甲、乙的位置还可以互换根据分步计数原理,得到结果;
(2)除甲乙两人外其余3人的排列数为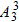 ,而甲乙二人应插其余3人排好的空才不相邻;且甲、乙位置可以互换.故有
,而甲乙二人应插其余3人排好的空才不相邻;且甲、乙位置可以互换.故有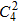
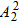 种排列方式;
种排列方式;
(3)若甲站最右端,则乙与其余三人可任意排,则此时的排法数为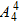 种;若甲不站最右端,则先从中间3个位置中选一个给甲,再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为
种;若甲不站最右端,则先从中间3个位置中选一个给甲,再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为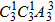 种;
种;
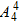 种,且甲、乙的位置还可以互换根据分步计数原理,得到结果;
种,且甲、乙的位置还可以互换根据分步计数原理,得到结果;(2)除甲乙两人外其余3人的排列数为
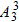 ,而甲乙二人应插其余3人排好的空才不相邻;且甲、乙位置可以互换.故有
,而甲乙二人应插其余3人排好的空才不相邻;且甲、乙位置可以互换.故有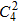
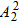 种排列方式;
种排列方式;(3)若甲站最右端,则乙与其余三人可任意排,则此时的排法数为
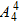 种;若甲不站最右端,则先从中间3个位置中选一个给甲,再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为
种;若甲不站最右端,则先从中间3个位置中选一个给甲,再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为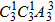 种;
种;(1)把甲乙捆绑成一个整体与其余3人当着4个人作全排列有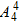 种,
种,
且甲、乙的位置还可以互换,
∴不同站法有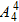
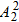 =48种.
=48种.
(2)除甲乙两人外其余3人的排列数为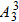 ,
,
而甲乙二人应插其余3人排好的空才不相邻;
且甲、乙位置可以互换.故有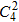
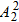 种排列方式.
种排列方式.
∴不同站法有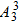 •
•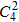
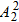 =72种.
=72种.
(3)优先考虑甲:
若甲站最右端,则乙与其余三人可任意排,则此时的排法数为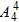 种;
种;
若甲不站最右端,则先从中间3个位置中选一个给甲,
再从除最右端的省余的3个位置给乙,其余的三个人任意排,
则此时的排法数为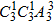 种;
种;
∴不同站法有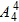 +
+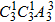 =78种.
=78种.
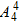 种,
种,且甲、乙的位置还可以互换,
∴不同站法有
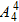
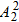 =48种.
=48种.(2)除甲乙两人外其余3人的排列数为
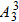 ,
,而甲乙二人应插其余3人排好的空才不相邻;
且甲、乙位置可以互换.故有
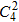
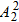 种排列方式.
种排列方式.∴不同站法有
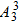 •
•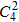
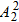 =72种.
=72种.(3)优先考虑甲:
若甲站最右端,则乙与其余三人可任意排,则此时的排法数为
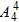 种;
种;若甲不站最右端,则先从中间3个位置中选一个给甲,
再从除最右端的省余的3个位置给乙,其余的三个人任意排,
则此时的排法数为
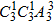 种;
种;∴不同站法有
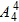 +
+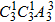 =78种.
=78种.【点评】本题考查排列组合的实际应用,是一个排列问题,注意相邻问题的排法,有限制条件的元素,要优先考虑.