古人曾研究过所谓的“多边形数”:即能用点排成多边形(通常排成正多边形)的阵列表示的数.在数学史上曾一度为不少专业和业余的数学家所青睐,人们认为这些奇妙的数一定有它特殊的性质,因为七们的确很具数学美.v图所示是前5个三角形数.第图个三角形数是图,第右个三角形数是3,第3个三角形数是q…,依此规律回答以v三个问题:(图)第q个三角形数是;(右)第地个三角形数是地(地+图)右地(地+图)右(用含地的式子表示,其中地表示正整数);(3)第右0图3个三角形数与右0图图个三角形数的差是.
2019-04-11
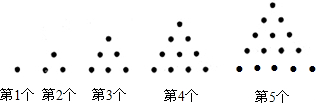
古人曾研究过所谓的“多边形数”:即能用点排成多边形(通常排成正多边形)的阵列表示的数.在数学史上曾一度为不少专业和业余的数学家所青睐,人们认为这些奇妙的数一定有它特殊的性质,因为七们的确很具数学美.v图所示是前5个三角形数.第图个三角形数是图,第右个三角形数是3,第3个三角形数是q…,依此规律回答以v三个问题:
(图)第q个三角形数是______;
(右)第地个三角形数是
(用含地的式子表示,其中地表示正整数);
(3)第右0图3个三角形数与右0图图个三角形数的差是______.
(图)第q个三角形数是______;
(右)第地个三角形数是
| 地(地+图) |
| 右 |
| 地(地+图) |
| 右 |
(3)第右0图3个三角形数与右0图图个三角形数的差是______.
