优质解答
证明:
(1)
由:y(x)=
anxn,
得:y′(x)=
nanxn−1,y″(x)=
n(n−1)anxn−2=
(n+2)(n+1)an+2xn,
而和函数y(x)满足给定的微分方程,
于是代入y″-2xy′-4y=0,得:
(n+2)(n+1)an+2xn−2x
nanxn−1−4
anxn=0,
比较xn的系数可得:
(n+2)(n+1)an+2-2nan-4an=0,
化简即得:an+2=
,n=1,2,3,…,证毕.
(2)
由y(0)=0,y′(0)=1,
可得到:a0=0,a1=1,
由(1)知:an+2=
,
可以得出an的表达式为:an=
,
因此:
y(x)=x+x3+
(1)
由:y(x)=
| ∞ |
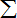 |
| n=0 |
得:y′(x)=
| ∞ |
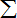 |
| n=1 |
| ∞ |
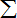 |
| n=2 |
| ∞ |
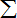 |
| n=0 |
而和函数y(x)满足给定的微分方程,
于是代入y″-2xy′-4y=0,得:
| ∞ |
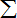 |
| n=0 |
| ∞ |
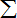 |
| n=1 |
| ∞ |
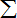 |
| n=0 |
比较xn的系数可得:
(n+2)(n+1)an+2-2nan-4an=0,
化简即得:an+2=
| 2an |
| n+1 |
(2)
由y(0)=0,y′(0)=1,
可得到:a0=0,a1=1,
由(1)知:an+2=
| 2an |
| n+1 |
可以得出an的表达式为:an=
|
因此:
y(x)=x+x3+
xy(x)=
得:y′(x)=
而和函数y(x)满足给定的微分方程, 于是代入y″-2xy′-4y=0,得:
比较xn的系数可得: (n+2)(n+1)an+2-2nan-4an=0, 化简即得:an+2=
(2) 由y(0)=0,y′(0)=1, 可得到:a0=0,a1=1, 由(1)知:an+2=
可以得出an的表达式为:an=
因此: y(x)=x+x3+ |