如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,-5). (1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
2019-05-07
如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,-5).
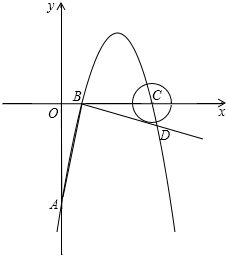
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
优质解答
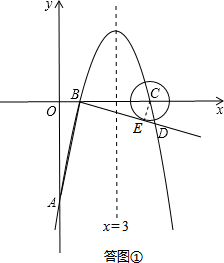 (1)设抛物线解析式为:y=a(x-3)2+4,
(1)设抛物线解析式为:y=a(x-3)2+4,
将A(0,-5)代入求得:a=-1,
∴抛物线解析式为y=-(x-3)2+4=-x2+6x-5.
(2)抛物线的对称轴l与⊙C相离.证明:
令y=0,即-x2+6x-5=0,得x=1或x=5,
∴B(1,0),C(5,0).
如答图①所示,设切点为E,连接CE,
由题意易证Rt△ABO∽Rt△BCE,
∴=,
即=,
求得⊙C的半径CE===;
而点C到对称轴x=3的距离为2,2>,
∴抛物线的对称轴l与⊙C相离.
(3)存在.理由如下: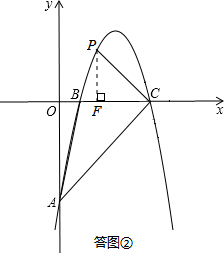
有两种情况:
(I)如答图②所示,点P在x轴上方.
∵A(0,-5),C(5,0),
∴△AOC为等腰直角三角形,∠OCA=45°;
∵PC⊥AC,∴∠PCO=45°.
过点P作PF⊥x轴于点F,则△PCF为等腰直角三角形.
设点P坐标为(m,n),则有OF=m,PF=CF=n,
OC=OF+CF=m+n=5 ①
又点P在抛物线上,
∴n=-m2+6m-5 ②
联立①②式,解得:m=2或m=5.
当m=5时,点F与点C重合,故舍去,
∴m=2,
∴n=3,
∴点P坐标为(2,3);
(II)如答图③所示,点P在x轴下方.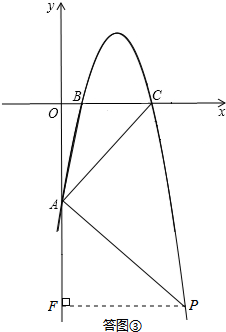
∵A(0,-5),C(5,0),
∴△AOC为等腰直角三角形,∠OAC=45°;
过点P作PF⊥y轴于点F,
∵PA⊥AC,
∴∠PAF=45°,即△PAF为等腰直角三角形.
设点P坐标为(m,n),则有PF=AF=m,OF=-n=OA+AF=5+m,
∴m+n=-5 ①
又点P在抛物线上,
∴n=-m2+6m-5 ②
联立①②式,解得:m=0或m=7.
当m=0时,点F与原点重合,故舍去,
∴m=7,
∴n=-12,
∴点P坐标为(7,-12).
综上所述,存在点P,使△ACP是以AC为直角边的直角三角形.点P的坐标为(2,3)或(7,-12).
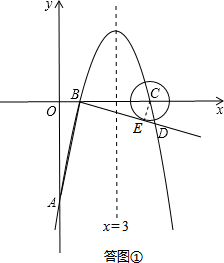 (1)设抛物线解析式为:y=a(x-3)2+4,
(1)设抛物线解析式为:y=a(x-3)2+4,
将A(0,-5)代入求得:a=-1,
∴抛物线解析式为y=-(x-3)2+4=-x2+6x-5.
(2)抛物线的对称轴l与⊙C相离.证明:
令y=0,即-x2+6x-5=0,得x=1或x=5,
∴B(1,0),C(5,0).
如答图①所示,设切点为E,连接CE,
由题意易证Rt△ABO∽Rt△BCE,
∴=,
即=,
求得⊙C的半径CE===;
而点C到对称轴x=3的距离为2,2>,
∴抛物线的对称轴l与⊙C相离.
(3)存在.理由如下:
有两种情况:
(I)如答图②所示,点P在x轴上方.
∵A(0,-5),C(5,0),
∴△AOC为等腰直角三角形,∠OCA=45°;
∵PC⊥AC,∴∠PCO=45°.
过点P作PF⊥x轴于点F,则△PCF为等腰直角三角形.
设点P坐标为(m,n),则有OF=m,PF=CF=n,
OC=OF+CF=m+n=5 ①
又点P在抛物线上,
∴n=-m2+6m-5 ②
联立①②式,解得:m=2或m=5.
当m=5时,点F与点C重合,故舍去,
∴m=2,
∴n=3,
∴点P坐标为(2,3);
(II)如答图③所示,点P在x轴下方.
∵A(0,-5),C(5,0),
∴△AOC为等腰直角三角形,∠OAC=45°;
过点P作PF⊥y轴于点F,
∵PA⊥AC,
∴∠PAF=45°,即△PAF为等腰直角三角形.
设点P坐标为(m,n),则有PF=AF=m,OF=-n=OA+AF=5+m,
∴m+n=-5 ①
又点P在抛物线上,
∴n=-m2+6m-5 ②
联立①②式,解得:m=0或m=7.
当m=0时,点F与原点重合,故舍去,
∴m=7,
∴n=-12,
∴点P坐标为(7,-12).
综上所述,存在点P,使△ACP是以AC为直角边的直角三角形.点P的坐标为(2,3)或(7,-12).


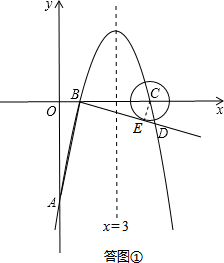 (1)设抛物线解析式为:y=a(x-3)2+4,
(1)设抛物线解析式为:y=a(x-3)2+4,
