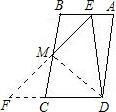
如图所示.▱ABCD中,DE⊥AB于E,BM=MC=DC.求证:∠EMC=3∠BEM.
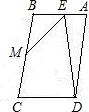 如图所示.▱ABCD中,DE⊥AB于E,BM=MC=DC.求证:∠EMC=3∠BEM.
如图所示.▱ABCD中,DE⊥AB于E,BM=MC=DC.求证:∠EMC=3∠BEM.
2019-05-28
 如图所示.▱ABCD中,DE⊥AB于E,BM=MC=DC.求证:∠EMC=3∠BEM.
如图所示.▱ABCD中,DE⊥AB于E,BM=MC=DC.求证:∠EMC=3∠BEM.
2019-05-28
 如图所示.▱ABCD中,DE⊥AB于E,BM=MC=DC.求证:∠EMC=3∠BEM.
如图所示.▱ABCD中,DE⊥AB于E,BM=MC=DC.求证:∠EMC=3∠BEM.