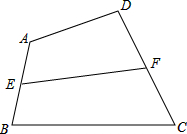
如图,四边形ABCD中,点E,F分别是AB、DC的中点,试说明:AD+BC>2EF.
2019-04-22
如图,四边形ABCD中,点E,F分别是AB、DC的中点,试说明:AD+BC>2EF.

2019-04-22

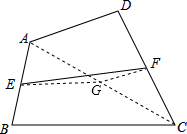 证明:如图,连接AC,取AC的中点G,连接EG、FG,
证明:如图,连接AC,取AC的中点G,连接EG、FG, 证明:如图,连接AC,取AC的中点G,连接EG、FG,
证明:如图,连接AC,取AC的中点G,连接EG、FG,